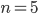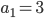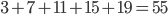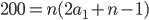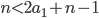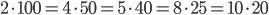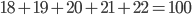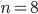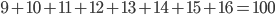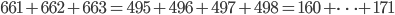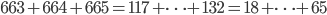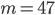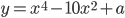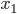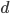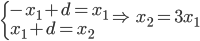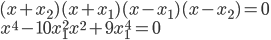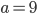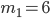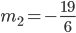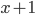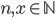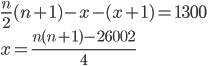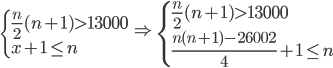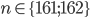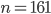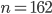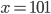- Dělník vyrobí za den 26 součástek. Kdyby zvyšoval výkon denně o 1 součástku, kolik vyrobí za 18 dní?
Řešení ukaž - Jarda má dvoukorunové mince. Uspořádal je do lichoběžníku tak, že každá následující řada má o jednu mince méně. V první řadě bylo 90 mincí, v poslední řadě 3 mince. Kolik má Jarda peněz?
Řešení ukaž - Turista stoupající na horu vystoupal za první hodinu do výšky 800 m. Každou další hodinu pak zdolá výšku o 25 m menší než předcházející hodinu. Za kolik hodin se dostane na vrchol ve výšce 5700 m?
Řešení ukaž - V soutěži byly za prvních 6 míst vyplaceny odměny v celkové hodnotě 2400 Kč. Nejvyšší odměna byla za první místo, za další umístění se odměny postupně snižovaly, vždy o stejnou částku 100 Kč. Jaká byla cena za první místo?
Řešení ukaž - 300 dolarů máme rozdělit pěti dělníkům tak, aby druhý dělník dostal o tolik dolarů více než první, o kolik třetí dostal více než druhý, čtvrtý než třetí a pátý než čtvrtý. První dva dělníci mají dostat sedmkrát méně dolarů než ostatní tři. Kolik dolarů má dostat každý dělník?
Řešení ukaž - Stromek byl zasazený, když byl vysoký 40 cm. Každý rok vyrostl vždy o stejnou výšku. Na konci 6. roku byl dvakrát vyšší než na konci 2. roku. Jak vysoký byl stromek na konci 4. roku?
Řešení ukaž - Parta dětí vlezla do zahrady a děti začaly trhat jablka. První utrhlo jedno jablko, druhé dvě a každé další o jedno jablko více než to předcházející. Potom se všichni, kdo trhali jablka, rozdělili rovným dílem a každý dostal šest jablek. Kolik dětí trhalo jablka?
Řešení ukaž - Roku 1620 začal pan Rich ukládat do banky peníze. Každý rok uložil tolik liber, jaký byl rok (tj. roku 1620 uložil 1620 liber, roku 1621 uložil 1621 liber atd.). V této činnosti pokračují jeho potomkové dodnes. Kolik peněz měli v bance v roce 2000?
Řešení ukaž - Od svých desátých narozenin dostává Arnold od rodičů kapesné. Každý měsíc dostane dvakrát tolik euro, kolik je mu let. Kolik peněz měl naštřeno den před 18. narozeninami, když šetří 25 % toho, co dostane?
Řešení ukaž - 31 knih je seřazeno do řady od nejlevnější (vlevo) po nejdražší (vpravo). Rozdíl ceny dvou sousedních knih je vždy 2 Kč. Za cenu, kterou má nejdražší kniha, můžeme koupit prostřední knihu a k ní sousední knihu. Kolik stojí nejlevnější kniha?
Řešení ukaž - Jednotlivé díly sedmidílného románu byly vydávány v devítiletých intervalech. Když byl vydán sedmý díl, byl součet roků vydání jednotlivých dílů 13 601. Ve kterém roce byl vydán pátý díl?
Řešení ukaž - Lupiči první den ukradli z 1. trezoru určité množství peněz. Druhý den ukradli z 2. trezoru dvakrát více peněz, třetí den ze 3. trezoru třikrát více peněz atd. až stý den ze 100. trezoru ukradli 100krát více peněz a v trezoru zůstala 1 Kč. Přitom ve všech trezorech zůstalo dohromady 24 850 Kč. Kolik peněz bylo původně v každém trezoru, když ve všech trezorech bylo původně stejné množství peněz?
Řešení ukaž - V náhrdelníku 33 perel je prostřední perla nejdražší ze všech. Začneme-li z jednoho konce, je každá perla o 100$ dražší než předchozí až k prostřední perle. Z druhého konce je každá perla o 150$ dražší než předchozí až k prostřední perle. Celý náhrdelník stojí 65000$. Kolik stojí prostřední perla?
Řešení ukaž - V ZOO si připravili k nakrmení 31 lvů zásobu ovcí. Jeden lev sní 10 ovcí za týden. Jenže lvi onemocněli neznámou nemocí a každý týden jeden lev zemřel. Zásoba ovcí tak vydržela dvojnásobnou dobu, než bylo původně naplánováno. Kolik měli připraveno ovcí a na kolik týdnů měly původně stačit?
Řešení ukaž
- Strany pravoúhlého trojúhelníka tvoří aritmetickou posloupnost. Určete je, když obsah trojúhelníka je
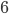 dm
dm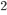 .
.
Řešení ukaž - Délky stran pravoúhlého trojúhelníku tvoří 3 po sobě jdoucí členy aritmetické posloupnosti. Delší odvěsna má délku 28 dm. Určete obvod a obsah trojúhelníka.
Řešení ukaž - Vnitřní úhly v konvexním čtyřúhelníku tvoří aritmetickou posloupnost. Největší úhel je o
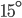 menší než dvojnásobek nejmenšího úhlu. Určete velikost největšího úhlu.
menší než dvojnásobek nejmenšího úhlu. Určete velikost největšího úhlu.
Řešení ukaž - Vnitřní úhly v konvexním čtyřúhelníku tvoří aritmetickou posloupnost. Největší úhel je dvakrát větší než nejmenší úhel. Určete velikost největšího úhlu.
Řešení ukaž - Vnitřní úhly konvexního devítiúhelníku tvoří aritmetickou posloupnost. Nejmenší úhel je
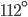 . Jak velký je největší úlel?
. Jak velký je největší úlel?
Řešení ukaž - Vnitřní úhly konvexního
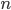 -úhelníku tvoří aritmetickou posloupnost s diferencí
-úhelníku tvoří aritmetickou posloupnost s diferencí 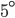 . Nejmenší úhel je
. Nejmenší úhel je 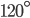 . Určete počet stran
. Určete počet stran 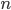 -úhelníka.
-úhelníka.
Řešení ukaž - Objem kvádru je 612 cm
 . Délky jeho hran jsou tři po sobě jdoucí členy aritmetické posloupnosti. Délka jedné z hran je 9 cm. Porovnejte povrchy kvádrů, které tyto podmínky splňují.
. Délky jeho hran jsou tři po sobě jdoucí členy aritmetické posloupnosti. Délka jedné z hran je 9 cm. Porovnejte povrchy kvádrů, které tyto podmínky splňují.
Řešení ukaž
- Kolik celých čísel mezi 100 a 1000 je dělitelných sedmi?
Řešení ukaž - Určete součet všech čísel od 1 do 100, která nejsou dělitelná čtyřmi.
Řešení ukaž - Určete součet všech přirozených čísel menších než 45, která nejsou dělitelná třemi.
Řešení ukaž - Určete počet čtyřciferných přirozených čísel, která jsou dělitelná třemi nebo sedmi.
Řešení ukaž
- Součet dvaceti po sobě jdoucích přirozených čísel je roven 510. Určete nejmenší z těchto čísel.
Řešení ukaž - Napište číslo 55 jako součet několika přirozených čísel tak, aby každé následující číslo bylo o 4 větší než předcházející.
Řešení ukaž - Najděte všechny množiny dvou nebo více za sebou jdoucích přirozených čísel, jejichž součet je 100.
Řešení ukaž - Napište všechny způsoby, kterými můžeme napsat číslo 1986 jakou součet po sobě jdoucích přirozených čísel.
Řešení ukaž - Napište všechny způsoby, kterými můžeme napsat číslo 1992 jakou součet po sobě jdoucích přirozených čísel.
Řešení ukaž - Součet několika přirozených po sobě jdoucích čísel je 2000. Jestliže
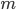 je první člen posloupnosti, určete nejmenší možnou hodnotu čísla
je první člen posloupnosti, určete nejmenší možnou hodnotu čísla 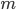 .
.
Řešení ukaž - Kořeny rovnice
 tvoří čtyři za sebou jdoucí členy aritmetické posloupnosti. Určete hodnotu parametru
tvoří čtyři za sebou jdoucí členy aritmetické posloupnosti. Určete hodnotu parametru 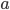 .
.
Řešení ukaž - Kořeny rovnice
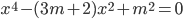 tvoří čtyři za sebou jdoucí členy aritmetické posloupnosti. Určete hodnotu parametru
tvoří čtyři za sebou jdoucí členy aritmetické posloupnosti. Určete hodnotu parametru 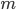 .
.
Řešení ukaž
- Neznámý vandal vytrhl z knihy jeden list. Součet čísel zbývajících stran je 13000. Kolik stran měla knížka? Jaká čísla byla na vytrženém listu?
Řešení ukaž - V jiné knize někdo vytrhl z první poloviny knihy dva sousední listy. Součet čísel zbývajících stran je 1054. Kolik stran měla knížka? Jaká čísla byla na vytržených listech?
Řešení ukaž
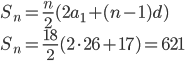
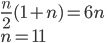
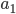
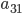
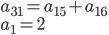
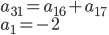
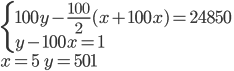
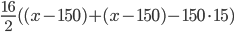
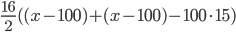
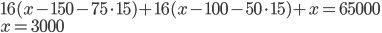
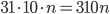
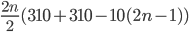
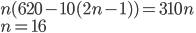
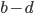
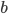
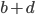
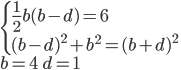
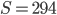
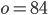
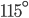
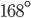
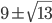
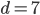
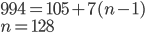
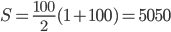
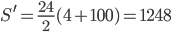
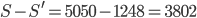
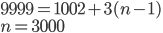
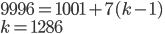
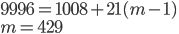
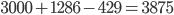
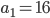
![55=\frac n2[a_1+a_1+4(n-1)]\\ n(a_1+2n-2)=55\cdot1=5\cdot11](http://su.rubesz.cz/wp-content/plugins/latex/cache/tex_373c3f4716a537c2df4b61fc7fe35965.gif)