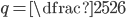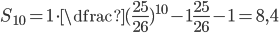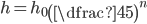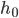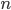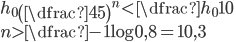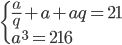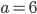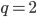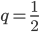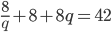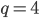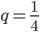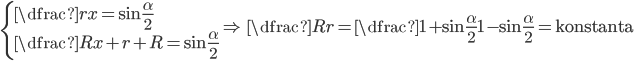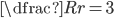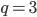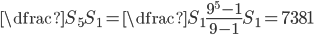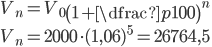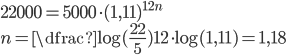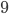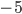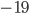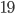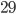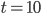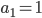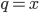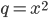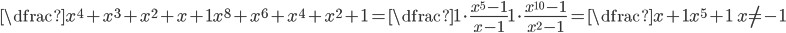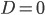- Honzův otec má sud, ve kterém bylo původně 26 litrů vína. Honza každý den nabral ze sudu 1 litr, který vypil. Aby otec nic nepoznal tak potom vždy do sudu nalil 1 litr vody. Kolik vína vypil Honza za 10 dní?
Řešení ukaž - Míč odskakuje po odrazu od vodorovné roviny do 4/5 výšky, ze které dopadl. Po kolika odrazech dostoupí do výšky menší, než je jedna desetina výšky ze které byl spuštěn?
Řešení ukaž - Gumová kulička volně puštěná z výšky 2 m se poprvé odrazí do výšky 1,9 m. Po kolikátém odrazu už nepřekoná výšku 1,5 m?
Řešení ukaž - Horkovzdušný balón vystoupá 25 metrů vysoko za minutu po startu. Každou další minutu vystoupá 75 % výšky, kterou vystoupal za předchozí minutu. Jak dlouho potrvá balónu, než bude více než 110 metrů vysoko?
Řešení ukaž
- Hrany kvádru tvoří geometrickou posloupnost. Součet délek tří různých hran je 21 cm, objem je 216 cm
 . Určete délky hran.
. Určete délky hran.
Řešení ukaž - Rozměry kvádru jsou po sobě jdoucí členy geometrické posloupnosti. Objem kvádru je 216 cm
 a povrch kvádru je 312 cm
a povrch kvádru je 312 cm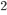 . Urči rozměry kvádru.
. Urči rozměry kvádru.
Řešení ukaž - Strany trojúhelníka tvoří geometrickou posloupnost. Obvod je 42 cm, délka prostřední strany je
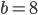 cm. Jaké jsou další strany?
cm. Jaké jsou další strany?
Řešení ukaž - Strany pravoúhlého trojúhelníka tvoří geometrickou posloupnost. Jaký je její kvocient?
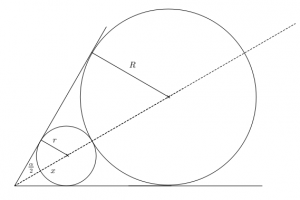
Řešení ukaž - Do úhlu, jehož ramena svírají
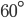 , je vepsáno pět kružnic tak, že každá následující (počínaje druhou) se dotýká předcházející kružnice. Kolikrát je součet ploch všech pěti kruhů větší než plocha prvního kruhu?
, je vepsáno pět kružnic tak, že každá následující (počínaje druhou) se dotýká předcházející kružnice. Kolikrát je součet ploch všech pěti kruhů větší než plocha prvního kruhu?
Řešení ukaž
- Uložíme do banky 2 000$. Banka platí roční úrok 6 %. Kolik budeme mít v bance za 5 let?
Řešení ukaž - Kolik let je potřeba, aby se vklad 5 000 Kč zvětšil na 22 000 Kč, když úrok je 11 % měsíčně?
Řešení ukaž - Podnikatel si půjčil v bance 200 000 Kč na 5 let s 15% úrokem. Jakou částku zaplatí, když celý dluh splatí naráz po pěti letech?
Řešení ukaž - Nový dům má cenu 2 500 000 Kč. Každý rok ztrácí 10 % své hodnoty. Za kolik let bude mít cenu 250 000 Kč?
Řešení ukaž - Nákupní cena auta je 250 000 Kč. Jaká bude jeho hodnota za 3 roky, když se ročně odepisuje 11,5 % na amortizaci? Za jakou dobu klesne cena na polovinu?
Řešení ukaž - Sbírka známek měla v roce 1987 cenu 80 Kč. Do roku 1997 vzrostla cena na 200 Kč. Ve kterém roce bude cena známek 20 000 Kč, když cena poroste exponenciálně stále stejným tempem?
Řešení ukaž - Spotřeba uhlí rostla mezi roky 1947 až 1971 o 3,1 % ročně. Při spotřebě uhlí, která byla v roce 1972, by zásoby uhlí vydržely 600 roků. Na kolik roků vydrží zásoby uhlí, když spotřeba bude růst stále o 3,1 % ročně?
Řešení ukaž - Firma se rozhodla na začátku roku, že v každém čtvrtletí zvýší svůj obrat o 2 %.
a) O kolik procent se zvýší obrat firmy za dva roky?
b) Za jak dlouho vzroste obrat firmy o 25 %?Řešení ukaž - Průlněrnou rodinu stalo v roce 2000 zdravotní pojištění 300$ za měsíc. Kolik bude stát v roce 2050, když očekávanát inflace bude 8 % ročně?
Řešení ukaž - Lyžařské středisko zahájilo činnost v roce 1963. V té době stál celodenní lístek na vlek 5$. Jeho cena se každoročně zvyšovala o 7 %. Kolik stál v roce 1993?
Řešení ukaž - Za pět let se počet obyvatel ve městě zvýšil 0 12 %. Jaký byl roční procentuální přírůstek obyvatelstva?
Řešení ukaž - Počet obyvatel města vzrostl za 15 let z 48 000 obyvatel na 61 500 obyvatel. Jaký byl roční přírůstek v procentech? Kolik obyvatel lze očekávat ve městě za dalších 10 let při stejném ročním procentuálním přírůstku?
Řešení ukaž
- Kolik peněz bude mít v bance člověk po 10-ti letech, když tam na začátku každého roku vloží 2000 Kč. Roční úrok je 3 %.
- Pan Starý má půjčku 300 000 Kč na roční úrok 14 %. Jaká musí být každoroční splátka dluhu koncem roku, chce-li pan Starý splatit dluh za pět let?
- Pan Nový může každý rok splácet koncem roku 50 000 Kč. Jak velkou půjčku si může vzít na roční úrok 15 %, když chce půjčku splatit za 20 let?
- Pan Šťastný vyhrál v loterii 3 000 000 Kč. Začátkem roku peníze uložil do banky na 9% roční úrok. Kolik peněz může na konci každého roku vybrat, jestliže chce vybírat vždy stejnou částku a chce, aby po 30ti letech neměl v bance žádné peníze?
- V bance je na 8% úrok uložen jeden milión korun. Jakou konstantní částku (přesností na haléře) musíte každý rok z banky vyzvednout, abyste měli za 20 let (tedy dvacet vyzvednutí této částky) konto s nulovým zůstatkem?
- V geometrické posloupnosti je součet prvních dvou členů 40, prvních tří 76 a prvních čtyř 130. Mezi prvními dvaceti členy najděte všechny, které mají celočíselnou hodnotu.
Řešení ukaž - Posloupnost tří reálných čísel tvoří aritmetickou posloupnost s prvním členem 9. Když k druhému členu přičteme 2 a ke třetímu přičteme 20, vzniknou tři za sebou jdoucí členy geometrické posloupnost. Určete původní čísla.
Řešení ukaž - Součin tří zasebou jdoucích členů geometrické posloupnosti je 216. Jejich součet je 19. Která jsou to čísla?
Řešení ukaž - V geometrické posloupnosti je
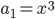 ,
, 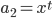 a
a 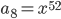 . Určete hodnotu
. Určete hodnotu 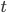 .
.
Řešení ukaž - Najděte čtyři čísla, která tvoří geometrickou posloupnost takovou, že součet krajních členů je roven 65 a součet prostředních členů je roven 20.
Řešení ukaž - Zjednodušte:
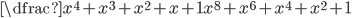
Řešení ukaž - Koeficienty
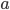 ,
, 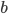 ,
,  kvadratické rovnice
kvadratické rovnice
tvoří tři za sebou jdoucí členy geometrické posloupnosti. Vypočítejte diskriminant rovnice.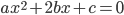
Řešení ukaž