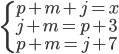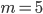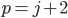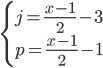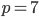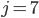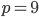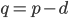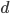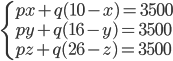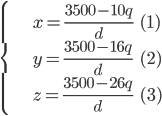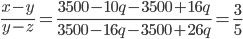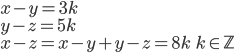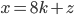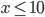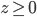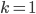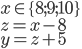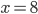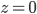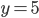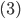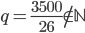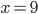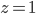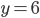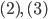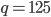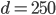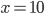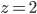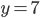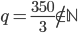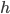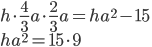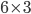- Farmář koupil několik koz za 17 € a několik ovcí za 19 €. Celkem zaplatil 201 €. Kolik koz a kolik ovcí koupil?
Řešení ukaž - Žena má v peněžence 2,15$ v drobných. Má jen deseticenty a dvacetipěticenty. Přitom má dvacetipěticentů více než deseticentů. Kolik mincí má v peněžence?
Řešení ukaž - V prodejně suvenýrů prodávají dva druhy trpaslíků. Jeden po 330 Kč a druhý po 450 Kč. Přijel autobus turistů a ti nakoupili trpaslíky za 5670 Kč. Kolik kterých trpaslíků koupili?
Řešení ukaž - Alena nakoupila pera po 10 Kč, štětce po 5 Kč a sešity po 2 Kč, dohromady 18 kusů, celkem za 100 Kč. Kolik čeho nakoupila?
Řešení ukaž - Pan Novák si kupuje trička a kravaty. Jedno tričko stojí 70 Kč a jedna kravata stojí 30 Kč. Celkem utratil pan Novák 810 Kč a koupil maximální možný počet triček. Kolik kusů celkem nakoupil?
Řešení ukaž - Jste správce tělocvičny a máte nakoupit míče dvou druhů, libovolného počtu. Malý stojí 320,-Kč a velký stojí 360,-Kč. Musíte utratit přesně 12000,-Kč. Kolik kterých míčů nakoupíte?
Řešení ukaž - Kapesníky stojí 3 Kč, ponožky 7 Kč a trička 16 Kč. Kolik kapesníků, ponožek a triček jsem nakoupil přesně za 50 Kč, když jsem od každého měl aspoň jeden kus?
Řešení ukaž - Skupina přátel byla v restauraci. Každá žena zaplatila útratu 1000 Kč a každý muž 1500 Kč. Celková útrata byla 12 000 Kč. Kolik žen a kolik mužů bylo ve skupině, když rozdíl mezi počtem mužů a počtem žen byl nejmenší možný?
Řešení ukaž - Do kasina přišel muž, který měl několik dvacetikorun a několik korun. Dohromady nebylo mincí ani dvacet. Muž všechno vsadil a vyhrál. Když spočítal nyní peníze, zjistil, že má 6krát víc peněz. Také zjistil, že má tolik dvacetikorun, kolik měl předtím korun a naopak. Kolik měl původně peněz?
Řešení ukaž - Součet dvouciferného čísla a čtyřnásobku jeho ciferného součtu je 122. Určete toto číslo.
Řešení ukaž - 100$ rozdělíme mezi 100 lidí tak, že každý muž dostane 3$, každá žena 2$ a každé dítě
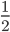 $. Kolik bylo dětí, když mužů byl lichý počet a bylo jich více než žen.
$. Kolik bylo dětí, když mužů byl lichý počet a bylo jich více než žen.
Řešení ukaž - Dvanáct lidí, mezi nimiž jsou dospělí muži, dospělé ženy a děti, nese 12 chlebů. Každý dospělý muž nese 2 chleby, každá dospělá žena nese
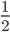 chleba a každé dítě nese
chleba a každé dítě nese 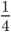 chleba. Kolik mužů, žen a dětí je ve skupině?
chleba. Kolik mužů, žen a dětí je ve skupině?
Řešení ukaž - Marie má 200 Kč v pěti-, deseti- a dvacetikorunách. Má stejný počet pěti- a desetikorun. Přitom má nejmenší možný počet mincí. Kolik má dvacetikorun?
Řešení ukaž - John má 4,55$ v drobných. Má jen deseticenty a dvacetipěticenty. Jaké největší a jaké nejmenší množství mincí může mít? Může mít obou druhů mincí stejné množství?
Řešení ukaž - V ZOO mají slony. Součet jejich věků dává po dělení pěti zbytek 4 a po dělení 9 zbytek 8. Všech osm slonů je stejně starých. Zcela jistě jim není více než 60? Jak jsou sloni staří?
Řešení ukaž - Na Dračím ostrově žilo 103 modrých a 113 zelených draků. Zlý čaroděj ostrov zaklel: Když se setkají 3 draci jedné barvy s 5 draky druhé barvy, všech 8 draků zmizí. Po určité době na ostrově zůstali jenom modří draci. Kolik byjich bylo?
Řešení ukaž - Za 100 korun nakoupíme poštovní známky V hodnotě 10 Kč, 3 Kč a 0,50 Kč (od každé alespoň jednu). Známek je dohromady 100. Kolik kterých známek jsme koupili?
Řešení ukaž - Vstupenky na školní ples stojí pro žáky 30 Kč, pro jejich rodiče 80 Kč a pro všechny ostatní 120 Kč. Na vstupném se vybralo přesně 3760 Kč a prodalo se právě 100 vstupenek. Kolik rodičů přišlo na ples?
Řešení ukaž - Písemná práce z matematiky obsahuje 26 otázek ve třech skupinách. První skupina je hodnocena 3 body, druhá 5 a třetí 8 body. Maximální počet bodů je 111. Kolik otázek je v jednotlivých skupinách, když otázek za 3 body je nejvíce a za 8 bodů nejméně?
Řešení ukaž - Divadelní soubor uvedl během sezony podle plánu třicet „Večerů s improvizacemi“. Fany, obdivovatelka hlavního protagonisty, si na začátku sezony spočítala, kolik by celkem utratila za vstupné, kdyby chodila na každé představení. Po několika uvedeních však bylo vstupné nečekaně zdraženo o 60 Kč. Později získal soubor významného sponzora a tuto novou cenu vstupného snížil o 85 Kč. Na konci sezony mohla Fany říci, že nevynechala ani jedno uvedení pořadu a za vstupné celkem utratila přesně tolik, kolik vypočítala na začátku sezony. Kolikrát Fany navštívila představení za vstupné v původní výši?
Řešení ukaž - Máme určité množství stejných kostek. Víme, že je jich mezi 8000 a 10000. Když z nich sestavíme sloupec se základnou
 , v poslední vrstvě byly jen 2 kocky. Při stavění sloupců se základnou
, v poslední vrstvě byly jen 2 kocky. Při stavění sloupců se základnou 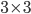 , nebo
, nebo 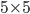 zůstaly v poslední vrstvě 4 kostky. Kolik kostek máme?
zůstaly v poslední vrstvě 4 kostky. Kolik kostek máme?
Řešení ukaž - Král choval čtyřicetinožky obrovské jednohlavé a trojhlavé draky vícenohé. Jeho stádo mělo 53 hlav a 622 nohou. Kolik nohou má drak?
Řešení ukaž - Na farmě je několik slepic, několik psů a několik bezhlavých trojnohých mimozemšťanů (tj. aspoň jeden od každého druhu). Dohromady mají 10 hlav a 43 nohou. Kolik mimozemšťanů je na farmě, když psů je nejvíce?
Řešení ukaž - Čtyřicetihlavé stádo volů, krav a telat má cenu 600 zlaťáků. Voli jsou po 18 zlaťácích, krávy po 15 a telata po 10. Určete kolik je kterých, víte-li, že krávy tvoří nejpočetnější skupinu, ale není jich více než volů a telat dohromady.
Řešení ukaž - Farmář prodal stohlavé stádo dobytka za 4000$. Krávy byly za 120$/kus, ovce za 50$/kus a prasata za 25$/kus. Od každého druhu byl ve stádu aspoň jeden kus. Jaké mohlo být složení stáda?
Řešení ukaž - Eratostenes šel do Alexandrie a cestou na trhu koupil kohouty, slepice a malá kuřátka. Celkem nakoupil 100 kusů drůbeže za 100 denárů. Kolik koupil slepic, kohoutů a kuřat, jestliže kohout stál 5 denárů, slepice 3 denáry a 3 kuřátka stála 1 denár? Najdi všechna řešení!
Řešení ukaž - Můj otec se narodil ve dvacátém století. Ciferný součet letopočtu jeho narození určuje, kolik mu bylo let v roce 1954. Kolik mu bylo let v roce 2000?
Řešení ukaž - Na otázku, jak je stará, odpověděla jedna milá stará paní: "Každá z cifer mého věku udává věk mých dvou vnuků. Jestliže sečtete věky obou vnuků a můj, dostanete číslo 83." Tak jak byla stará a jak její vnuci?
Řešení ukaž - Taneční kurs navštěvoval stejný počet chlapců i dívek. Na závěrečný večer přinesl každý chlapec pro každou dívku dárek. Chlapci přišli všichni, ale některé dívky zůstaly doma. Po obdarování přítomných dívek zůstalo 115 dárků. Kolik chlapců navštěvovalo kurs a kolik dívek zůstalo doma?
Řešení ukaž - Na oslavě narozenin byl průměrný věk
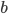 chlapců
chlapců 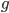 roků. Průměrný věk
roků. Průměrný věk 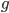 dívek byl
dívek byl 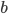 roků. Průměrný věk všech i s 42letým rodičem byl
roků. Průměrný věk všech i s 42letým rodičem byl 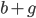 . Uřčete
. Uřčete 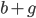 .
.
Řešení ukaž - Věk Petra, jeho mladšího bratra Jakuba a jejich babičky má tuto vlastnost: Když napíšeme Petrův věk před věk jeho babičky (té je méně než 100 let) dostaneme čtyřciferné číslo, které je stejné jako součin všech tří věků. Kolik je Petrovi?
Řešení ukaž - Obsah lichoběžníka je 1400. Jeho výška je 50. Základny
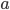 ,
,  ,
, 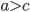 jsou celá čísla dělitelná osmi. Jaký je počet dvojic
jsou celá čísla dělitelná osmi. Jaký je počet dvojic ![[a;c]](http://su.rubesz.cz/wp-content/plugins/latex/cache/tex_7d860b5ba230e2cfcdc61d2121978c3a.gif) , které splňují dané podmínky?
, které splňují dané podmínky?
Řešení ukaž - Jeden člověk se narodil v první polovině 19. století. V roce
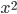 mu bylo
mu bylo 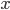 roků. Jaký je rok jeho narození?
roků. Jaký je rok jeho narození?
Řešení ukaž - Součin číslic věku Aleše je stejné nenulové číslo, jako bylo před šesti lety. Za kolik let se to stane opět?
Řešení ukaž - Josef se vracel z výletu. Nejprve jel vlakem a pak pokračoval na kole. Celá cesta mu trvala 1,5 hodiny a urazil při ní 60 km. Vlak jel průměrnou rychlostí 50 km/h. Určete, jak dlouho jel Josef na kole, když jeho rychlost v km/h je vyjádřena přirozeným číslem stejně jako vzdálenost v km, kterou na kole ujel a jel nejvyšší možnou rychlostí, která daným podmínkám vyhovuje.
Řešení ukaž - Zjistěte, které dvojice pravidelných mnohoúhelníků mají velikosti vnitřních úhlů v poměru
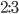 .
.
Řešení ukaž - Máme určitý počet krabiček a určitý počet kuliček. Dáme-li do každé krabičky právě jednu kuličku, zbyde nám
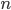 kuliček. Když však dáme právě
kuliček. Když však dáme právě 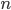 krabiček stranou, můžeme všechny kuličky rozmístit tak, aby jich v každé zbývající krabičce bylo právě
krabiček stranou, můžeme všechny kuličky rozmístit tak, aby jich v každé zbývající krabičce bylo právě 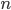 . Kolik máme krabiček a kolik kuliček?
. Kolik máme krabiček a kolik kuliček?
Řešení ukaž - Nováková, Vaňková a Sudková vyhrály štafetu a kromě diplomů dostaly i bonboniéru, kterou hned po závodech sluply. Kdyby snědla Petra 0 3 bonbóny vice, snědla by jich právě tolik, co Míša s Janou dohromady. A kdyby si Jana pochutnala ještě na sedmi bonbónech, také by jich měla tolik, co druhé dvě dohromady. Ještě víme, že počet bonbónů, které snědla Vaňková, je dělitelný třemi a že Sudková si smlsla na sedmi bonbónech. Jak se děvčata jmenovala? Kolik bonbónů snědla každá z nich?
Řešení ukaž - Tři farmáři prodávali na trhu kuřata. Jeden farmář měl 10 kuřat, druhý 16 a třetí 26. Aby si nekonkurovali, dohodli se, že budou kuřata prodávat za stejnou cenu (v celých korunách). Sešli se při obědě a konstatovali, že kuřata nejdou moc na odbyt, a tak se dohodli, že sníží cenu, opět všichni stejně (a opět v celých korunách). Na konci dne zjistili, že prodali všechna kuřata a že všichni utržili za kuřata stejnou částku - 3500 Kč. Jaká byla cena před obědem a jaká po obědě?
Řešení ukaž - Žákyně počítala objem kvádru se čtvercovou podstavou a celočíselnými (v metrech) stranami. Když vypočítala součin výšky a jedné hrany podstavy zjistila, že hranu podstavy počítala omylem o jednu třetinu větší, než měla být. Rozhodla se tedy druhou hranu podstavy počítat o jednu třetinu menší. Když si pak kontrolovala výsledky, zjistila, že se její výsledek liší od správného výsledku o 15 m3. Jaké byly rozměry kvádru?
Řešení ukaž - Jaké rozměry (v celých číslech) musí mít obdélník, aby jeho obvod i obsah byly vyjádřené stejným číslem v příslušných délkových a plošných jednotkách?
Řešení ukaž
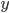
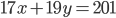
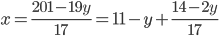
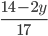
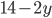
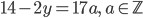
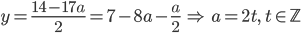
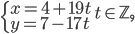
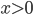
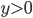
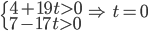
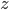
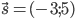
![[20;0]](http://su.rubesz.cz/wp-content/plugins/latex/cache/tex_a5ac4cab12a3ef2b2f07c4961cdb80a3.gif)
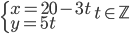
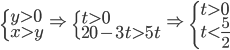
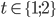
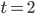
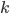

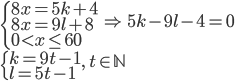
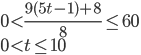

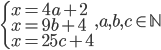
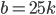
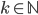
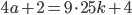
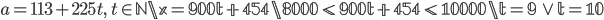
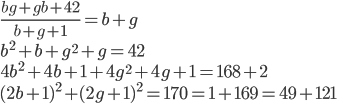
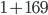
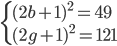
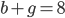
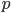
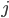
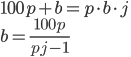
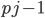
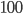
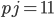
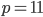
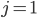
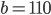
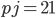
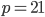
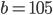
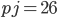
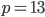
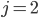
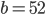
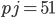
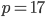
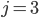
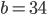
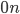
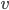
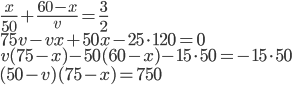
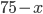
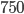
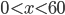
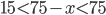
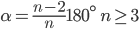
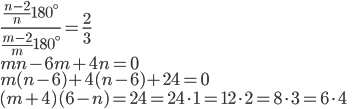
![[m;n]\in\{[20;5];[8;4];[4;3]\}](http://su.rubesz.cz/wp-content/plugins/latex/cache/tex_c0b9d9c6e46753509bdc0c76fe2cedb2.gif)