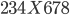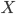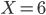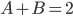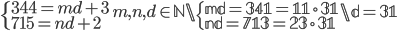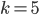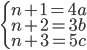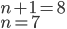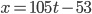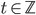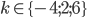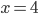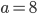1. Určete zbytek po dělení čísla 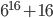6^{16}+16  pěti.
    Řešení ukaž
  2. V čísle 234X678 nahraďte X číslicí tak, aby vzniklo číslo dělitelné osmnácti.
    Řešení ukaž
  3. Jsou dána dvě přirozená čísla 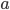a a 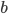b, která nejsou dělitelná třemi. Jaký je zbytek po dělení třemi čísla a^2+b^2?
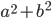    Řešení ukaž
  4. Které 5ticiferné číslo 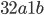32a1b je dělitelné 156? (Zde 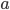a a 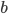b jsou cifry)
    Řešení ukaž

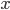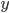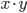  5. Přirozené číslo x má po dělení 1003 zbytek 21. Přirozené číslo y má po dělení 2006 zbytek 1000. Jaký zbytek po dělení 2006 má součin x\cdot y?

    Řešení ukaž

  6. Ke trojcifernému číslu 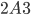2A3 přičteme 326. Výsledné trojciferné číslo 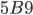5B9 je dělitelné devíti. Určete A+B.
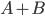    Řešení ukaž
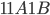  7.  Číslo 11A1B, kde písmena 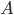A a 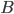B představují různé cifry, je dělitelné třemi. Kolika různých hodnot může nabývat součet A+B?
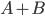    Řešení ukaž
  8. Když vydělíme číslo 344 číslem 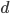d, bude zbytek 3. Když číslem 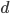d vydělíme 715, bude zbytek 2. Určete číslo d.
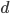    Řešení ukaž
  9. Najděte nejmenší čtyřciferné číslo složené z různých číslic takové, že je dělitelné každou ze svých číslic.
    Řešení ukaž
  10. Přirozené číslo 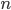n je dělitelné 5 . Totéž číslo 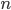n dává při dělení třemi zbytek 2. Urči nejmenší přirozené číslo 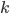k, které je třeba přičíst k číslu 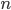n, aby byl součet 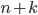n+k dělitelný 15.
    Řešení ukaž
  11. Mám trojciferné číslo. Když od něj odečtu 7, bude dělitelné sedmi. Když odečtu 8, bude dělitelné osmi a když odečtu 9, bude dělitelné devíti. Jaké je to číslo?
    Řešení ukaž
  12. Najděte nejmenší přirozené číslo 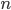n takové, že po dělení 3 dává zbytek 1, po dělení 5 dává zbytek 2 a po dělení 4 dává zbytek 3.
    Řešení ukaž
  13. Najděte nejmenší přirozené číslo, které dá při dělení třemi zbytek l, při dělení čtyřmi zbytek 2, při dělení pěti zbytek 3 a při dělení šesti zbytek 4. Které je to číslo?
    Řešení ukaž
  14. Určete nejmenší přirozené číslo 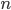n takové, že po dělení 5 dává zbytek 3, po dělení 9 dává zbytek 7 a po dělení 7 dává zbytek 4.
    Řešení ukaž
  15. Určete nejmenší přirozené číslo 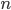n takové, že po dělení dvěma, třemi, čtyřmi, pěti i šesti dává zbytek 1 a přitom je dělitelné sedmi.
    Řešení ukaž
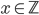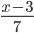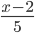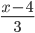  16. Pro jaká x\in\mathbb Z budou čísla \frac{x-3}{7}, \frac{x-2}{5} a \frac{x-4}{3} současně celými čísly?
    Řešení ukaž
  17. Určete všechna celá čísla 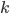k, pro která má rovnice

    (2k-1)x-3 = kx+2k

    s neznámou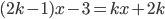 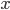x řešení v oboru přirozených čísel.
    Řešení ukaž
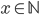  18. Najděte x\in\mathbb N a číslici 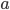a tak, aby platila rovnice

    [3\cdot(320+x)]^2=492a04.

    Řešení ukaž
  19. Dvě různá trojciferná čísla jsou obě dělitelná 21. Druhé z nich vznikne z prvního čísla tak, že zaměníme první cifru se třetí. Která jsou to čísla?
    Řešení ukaž