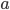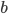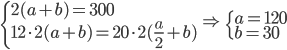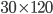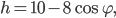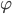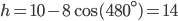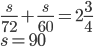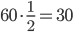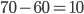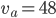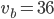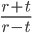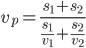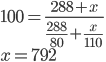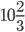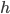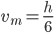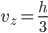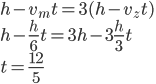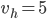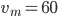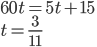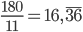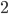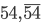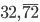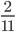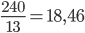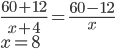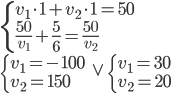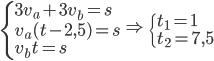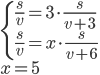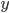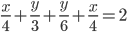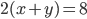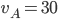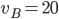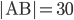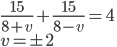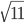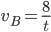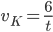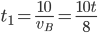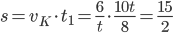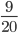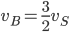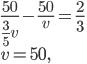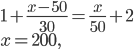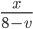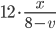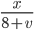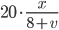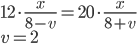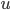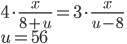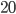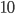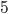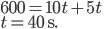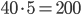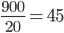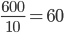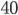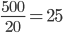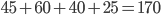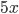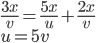- Tunelem dlouhým 1850 m projíždí vlak dlouhý 250 m rychlostí 80 km/h. Jak dlouho bude celý v tunelu?
Řešení ukaž - Vlak kolem mě přejede za 3 sekundy a most, který je dlouhý 75m, přejede za 6 sekund. Jak dlouhý je vlak?
Řešení ukaž - Rychlík vyjel z Prahy do Brna a jel bez zastávky rychlostí 60 km/h. Jiný vlak vyjel opačným směrem z Brna do Prahy a jel také bez zastávky, ale jen rychlostí 40 km/h. Jak daleko budou od vlaky hodinu před tím, než se setkají?
Řešení ukaž - Při duatlonu závodníci plavou 2 km a běží 10 km. Josef dokončí celý závod za 3 hodiny. Kdyby běžel rychlostí jakou plave a plaval rychlostí jakou běží, dokončil by závod za 7 hodin. Jakou rychlostí běží a jakou plave?
Řešení ukaž - Student chodí běhat kolem fotbalového hřiště tvaru obdélníku o obvodu 300 m. Vždy běhal stejnou rychlostí, ale někdy obíhal celé hřiště, někdy jen polovinu, když si cestu krátil po středové čáře. Zjistil, že celý okruh oběhne 12 krát za stejnou dobu jako 20 krát polovinu hřiště. Jaké jsou rozměry hřiště?
Řešení ukaž - Adam a Boris došli k přívozu na řece. Pro vyský stav vody se nepřeváželo. Věděli, že napravo i nalevo jsou lávky, ale nevěděli, která je blíže. Vydali se proto každý na jinou stranu. Oba šli stejnou rychlostí. Adam došel k lávce za hodinu, Boris za půl hodiny. Když lávky přešli (obě stejně dlouhé) pokračovali zpět směrem k sobě. Kde se potkali?
Řešení ukaž - Ruské kolo má poloměr 8 m a otáčí se o
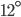 za sekundu. V čase
za sekundu. V čase 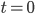 je jedna sedačka v nejnižší poloze 2 metry nad zemí. Určete v jaké výšce bude tato sedačka v čase 40 s.
je jedna sedačka v nejnižší poloze 2 metry nad zemí. Určete v jaké výšce bude tato sedačka v čase 40 s.
Řešení ukaž - Ruské kolo má poloměr 20 m a otáčí se konstantní rychlostí 1 ot./minutu. Za kolik sekund se dostane sedačka z nejnižší polohy do výšky 10 m nad nejnižší polohou?
Řešení ukaž - Na trati se míjejí dva protijedoucí vlaky stejné délky. První jede rychlostí 100 km/h, druhý 120 km/h. Cestující ve druhém vlaku vidí první vlak vedle sebe po dobu 6 s. Určete dobu, po kterou vidí cestující z prvního vlaku vedle sebe druhý vlak.
Řešení ukaž - Chovatel poštovních holubů se chtěl přesvědčit, zda se jeho holubi dovedou vrátit z neznámého místa do svého holubníku. Odvezl proto holuby autem do města N, kde je vypustil. Holubi se skutečně vrátili zpět, přitom od okamžiku, kdy chovatel s holuby vyjel, do okamžiku, kdy se vrátili do svého holubníku, uplynula doba 2 hodiny 45 minut. Vypočítejte vzdálenost města N od místa bydliště chovatele za předpokladu, že auto jelo rychlostí 72 km/h a holubi se vraceli zpět rychlostí 60 km/h.
Řešení ukaž
- Ema vyjela na výlet autem rychlostí 60 km/h. 30 minut po ní vyjel na stejnou trasu Pavel rychlostí 70 km/h. V jaké vzdálenosti od místa startu dohoní Pavel Emu?
Řešení ukaž - Z Milána do Vídně je to 240 km. Jedno auto vyjede z Milána do Vídně ve 12:00 rychlostí 55 km/h. Druhé auto vyjede z Vídně do Milána ve 13:00 rychlostí 45 km/h. V kolik hodin se setkají?
Řešení ukaž - Alice a Sylvie závodí v triatlonu - 2 km plavání, 40 km jízda na kole a nakonec 10 km běh. Obě vystartují v 8:00 a na každém úseku jsou jejich rychlosti konstantní. Alice zvládla plavání za 36 minut a na kole jela rychlostí 28 km/h. Sylvie zvládla plavání za 30 minut, ale na kole jela jen rychlostí 24 km/h. V kolik hodin dohonila Alice Sylvii?
Řešení ukaž - Cyklista jede třikrát větší rychlostí než jde chodec. Oba se pohybují po stejné trase a startují ze stejného místa. Cyklista vyjíždí čtvrt hodiny po odchodu chodce. Za jak dlouho od okamžiku, kdy vyjede cyklista, se setkají?
Řešení ukaž - Ze dvou míst
 a
a  , vzdálených od sebe 120 km, vyjedou současně 2 auta. Pohybují-li se proti sobě, je po 20 minutách jízdy mezi nimi vzdálenost 50 km. Vyjedou-li týmž směrem, pak po 24 minutáchje jejich vzdálenost 108 km. Vypočítejte, jakými rychlostmi se obě auta pohybují.
, vzdálených od sebe 120 km, vyjedou současně 2 auta. Pohybují-li se proti sobě, je po 20 minutách jízdy mezi nimi vzdálenost 50 km. Vyjedou-li týmž směrem, pak po 24 minutáchje jejich vzdálenost 108 km. Vypočítejte, jakými rychlostmi se obě auta pohybují.
Řešení ukaž - Dva povozy vyjely současně ze dvou míst 3 km vzdálených. Kdyby jely proti sobě, setkaly by se za 15 minut; kdyby však jely za sebou, dohonil by jeden druhý za 1 hodinu. Kolik metrů ujede každý z nich za minutu?
Řešení ukaž - Z města
 do města
do města  je to 1400 km. Jedné karavaně trvá překonání této vydálenosti o 30 dnů déle než druhé. Jaká je průměrná rychlost každé z karavan, pokud rozdíl těchto rychlostí ke 15 km/den?
je to 1400 km. Jedné karavaně trvá překonání této vydálenosti o 30 dnů déle než druhé. Jaká je průměrná rychlost každé z karavan, pokud rozdíl těchto rychlostí ke 15 km/den?
Řešení ukaž - Z kasáren vyjela kolona aut jedoucí průměrnou rychlostí 28 km/h do vojenského výcvikového prostoru a za 1h a 15 minut vyjelo za kolonou vojenské terénní vozidlo. Jelo průměrnou rychlostí 63 km/h a přijelo do výcvikového prostoru současně s kolonou. Určete vzdálenost vojenského výcvikového prostoru od kasáren.
Řešení ukaž - Jakub, Ken a Barbie začali ve stejný den řešit příklady z matematické sbírky. Každý pracoval konstatní rychlostí. Jakub řešil 12 úloh denně a dokončil sbírku 3 dny po Kenovi. Barbie vyřešila denně o tři problémy více než Ken a sbírku dokončila o dva dny dříve než Ken. Za kolik dní vyřešila sbírku Barbie?
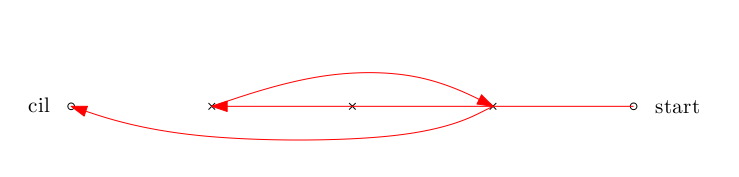
Řešení ukaž - Vzdálenost mezi Ostravou a Opavou je 36 km. Osobní automobil jel z Ostravy do Opavy o 15 minut kratší dobu než autobus. Rozdíl průměrných rychlostí osobního automobilu a autobusu byl 12 km/h. Určete průměrné rychlosti obou vozidel.
Řešení ukaž - Dva cyklisti jsou od sebe vzdáleni
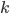 kilometrů. Startují ve stejný okamžik. Pokud jedou stejným směrem, setkají se za
kilometrů. Startují ve stejný okamžik. Pokud jedou stejným směrem, setkají se za 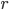 hodin. Pokud se pohybují směrem k sobě, setkají se za
hodin. Pokud se pohybují směrem k sobě, setkají se za 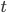 hodin. Jaký je poměr rychlosti rychlejšího a pomalejšího cyklisty?
hodin. Jaký je poměr rychlosti rychlejšího a pomalejšího cyklisty?
Řešení ukaž
- Auto jede prvních 288 km cesty rychlostí 80 km/h a zbytek cesty rychlostí 110 km/h. Průměrná rychlost na celé cestě byla 100 km/h. Jaká byla délka cesty?
Řešení ukaž - Klára jela na kole 4 km do kopce rychlostí 8 km/h, a pak 4 km dolů rychlostí 16 km/h. Jaká byla její průměrná rychlost?
Řešení ukaž - Cyklista jede
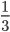 cesty do kopce rychlostí 16 km/h,
cesty do kopce rychlostí 16 km/h, 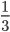 cesty po rovině rychlostí 24 km/h. Jakou rychlostí musí jet poslední
cesty po rovině rychlostí 24 km/h. Jakou rychlostí musí jet poslední 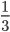 cesty z kopce, aby průměrná rychlost na celé trase byla 24 km/h?
cesty z kopce, aby průměrná rychlost na celé trase byla 24 km/h?
Řešení ukaž - Dvě auta jedou po stejné trase. První auto vyjelo v 7:15 a jelo průměrnou rychlostí 60 km/h. Druhé auto vyjelo v 7:30. Do cíle dojela obě auta současně v 8:15. Jaká byla průměrná rychlost druhého auta?
Řešení ukaž - Cyklista jede z
 do
do  proti větru rychlostí 10 km/h. Zpět z
proti větru rychlostí 10 km/h. Zpět z  do
do  jede po větru rychlostí 15 km/h. Jaká je jeho průměrná rychlost na celé cestě?
jede po větru rychlostí 15 km/h. Jaká je jeho průměrná rychlost na celé cestě?
Řešení ukaž - První část cyklistické trasy tvoří stoupání dlouhé 3 km, zbylou část klesání dlouhé 13 km. Pavlova průměrná rychlost na celé trase byla dvojnásobkem jeho rychlosti na první části trasy, jež byla o 16 km/h menší než na druhé části trasy. Za jak dlouho ujel Pavel celou trasu?
Řešení ukaž - Cesta ze školy je dlouhá 6 km. Kamil šel polovinu cesty rychlostí 4 km/h a druhou polovinu rychlostí 2 km/h. Naproti tomu šel Matěj rychlostí 4 km/h polovinu času, který potřeboval na cestu domů, a druhou polovinu časušel rychlostí 2 km/h. Který z nich byl dřív doma a o kolik minut?
Řešení ukaž - Petr jezdí každý den na kole stejnou trasu. První část jede do kopce rychlostí 9 km/h a druhou část z kopce rychlostí 22,5 km/h. Celkem ujede 45 km a jízda mu trvá 4 hodiny. Jak dlouho jede do kopce?
Řešení ukaž - Na cestě na dovolenou jsem jel 40 % cesty rychlostí 50 km/h a zbytek cesty rychlostí 100 km/h. Jaká byla moje průměrná rychlost na celé cestě?
Řešení ukaž
- Dvě svíčky, modrá a zelená, mají stejnou délku a byly zapáleny ve stejný okamžik. Modrá svíčka vyhoří za 6 hodin, zatímco zelená za 3 hodiny. Za jak dlouho po zapálení bude modrá svíčka třikrát delší než zelená?
Řešení ukaž - Máme dvě svíčky, které mají stejnou výšku, ale různou tloušťku. První vyhoří za 4 hodiny a druhá za 7 hodin. Ještliže obě svíčky hoří stejnoměrně, za jak dlouho bude mít první svíčka poloviční velikost než svíčka druhá?
Řešení ukaž - Máme zapálené dvě svíčky rozdílné výšky i objemu. Ta vyšší pokaždé vyhoří za tři a půl hodiny a ta menší za pět hodin. Ale za dvě hodiny jsou obě stejně vysoké. Věděli byste, v jakém poměru jsou jejich výšky před zapálením?
Řešení ukaž - Zapálili jsme současně dvě svíčky. Jedna z nich měřila 24 cm a dohoří za 2 hodiny. Druhá, kratší a silnější, měřila 12 cm a dohoří za 3 hodiny. Máme určit, ve kterém okamžiku měly obě hořící svíčky stejnou délku.
Řešení ukaž
- Za kolik minut od půlnoci budou svírat hodinová a minutová ručička 90°?
Řešení ukaž - Určete čas mezi 2:00 a 3:00, kdy minutová a hodinová ručička leží na jedné přímce.
Řešení ukaž - Student Ping Pong dělal domácí úkol mezi 16:00 a 17:00. Když začínal, byly minutová a hodinová ručička na sobě. Když skončil, byly ručičky přímo proti sobě. Kolik minut dělal Ping Pong domácí úkol?
Řešení ukaž - Za jak dlouho nejdříve po páté hodině budou minutová a hodinová ručička svírat pravý úhel?
Řešení ukaž - Přesně ve 3:00 hodin svírají hodinová a minutová ručička hodin úhel90°. Jaký je další nejbližší čas, kdy budou opět svírat úhel 90°?
Řešení ukaž - Nástěnné hodiny jsou seřízeny tak, že se v poledne hodinová, minutová i sekundová ručička přesně kryjí na dvanáctce. Dokážete spočítat přesný čas (na milisekundy), kdy se minutová a hodinová ručička budou opět překrývat?
Řešení ukaž - Kolik minut po 8:00 poprvé svírají minutová a hodinová ručička stejný úhel se svislou osou?
Řešení ukaž - Po okruhu běhají dva atleti, každý jinou konstantní rychlostí. Jesliže běží opačnými směry, potkávají se každých 10 minut. Jesliže běží stejným směrem, potkávají každých 40 minut. Za jakou dobu oběhne okruh rychlejší atlet?
Řešení ukaž
- Leonard dokáže vyřešit každou testovou otázku za 4 minuty zatímco Sheldon to dokáže za 1 minutu. Sheldon si uprostřed testu udělal hodinovou přestávku. Oba dokončili test současně. Kolik otázek měl test?
Řešení ukaž - Myš našla 1. února velký kus sýra ve tvaru kvádru a začala ho ohryzávat. Každý den ohryzala stejné množství sýra. Po měsíci (28 dní) jí zůstal kvádr s polovičními rozměry proti původnímu kvádru. Kolik dní jí sýr ještě vydrží?
Řešení ukaž - Mark a Bob startují ve stejnou dobu a jedou z Prahy do Libice (60 km). Mark jede rychlostí o 4 km/h menší než Bob. Bob se v Libici otočí a jede zpět. Potká Marka 12 km od Libice. Jaká je Markova rychlost?
Řešení ukaž - Dva cyklisti vyrazili z měst
 ,
,  proti sobě. Vzdálenost
proti sobě. Vzdálenost 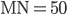 km. Cyklisti se setkali za 1 hodinu a pokračovali dále každý svým směrem. První z nich dorazil do
km. Cyklisti se setkali za 1 hodinu a pokračovali dále každý svým směrem. První z nich dorazil do  o 50 minut dříve, než druhý do
o 50 minut dříve, než druhý do  . Jaké byly rychlosti cyklistů?
. Jaké byly rychlosti cyklistů?
Řešení ukaž - Alice a Bill jdou proti sobě po stejné cestě z měst
 a
a  . Alice jde z
. Alice jde z  do
do  a Bill z
a Bill z  do
do  . Vyjdou ve stejný okamžik a potkají se za 3 hodiny. Alice pak dojde do
. Vyjdou ve stejný okamžik a potkají se za 3 hodiny. Alice pak dojde do  o 2,5 hodiny dříve než Bill do
o 2,5 hodiny dříve než Bill do  . Kolik hodin trvala Billova cesta?
. Kolik hodin trvala Billova cesta?
Řešení ukaž - Z města
 do města
do města  vzdáleného 240 km vyjel rychlostí 40 km/h autobus. Současně z města
vzdáleného 240 km vyjel rychlostí 40 km/h autobus. Současně z města  do
do  vyjelo auto rychlostí
vyjelo auto rychlostí 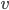 . Půl hodiny potom, co se minuly, se auto otočilo a stejnou rychlostí se vracelo do
. Půl hodiny potom, co se minuly, se auto otočilo a stejnou rychlostí se vracelo do  . Jaká byla rychlost
. Jaká byla rychlost 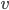 , když auto i autobus dorazily do
, když auto i autobus dorazily do  současně?
současně?
Řešení ukaž - Z Trutnova vyrazili dva cyklisté. Určete průměrnou rychlost každého z nich, víte-li, že ujeli 56 km a že pomalejší ztrácel na rychlejšího každou hodinu 2 km, takže přijel na místo určení o 30 minut později.
Řešení ukaž - Petr a Tomáš jeli na výlet na kole. Petr jel konstantní rychlostí 18 km/h a Tomáš jel konstantní rychlostí 19,5 km/h. Když Tomáš dojel do cíle, musel na Petra 20 minut čekat. Jak dlouhý byl výlet?
Řešení ukaž - Půjdu-li pohodlným tempem 4 km za hodinu, přijdu na nádraží 45 minut po odjezdu vlaku. Půjdu-li však průměrnou rychlostí 6 km za hodinu, na nádraží budu již půl hodiny před odjezdem vlaku. Jak daleko to mám na nádraží?
Řešení ukaž - Boris vyrazil pěšky na trať dlouhou 6 km. O nějaký čas později vyrazil na stejnou trať ze stejného místa Filip na kole. Filip jede třikrát rychleji, než jde Boris. Když Filip dohonil Borise, pokračoval do cíle trati,zatímco Boris se otočil a šel zpět ke startu. Filip dojel až na konec trati, otočil se a také se vrátil zpět ke startu. Do místa startu dorazili oba současně. Jak daleko od startu dohonil Filip Borise?
Řešení ukaž - Kája s Pepíkem bydlí ve městech vzdálených 48 km. Kája vyšel z domu ve 11 hodin. Pepík v 12 hodin. Setkali se přesně uprostřed cesty, protože měl Kája rychlost o 2 km/h větší než Pepík. Jakou měl Pepík rychlost?
Řešení ukaž - Franta a Honza byli právě v
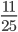 cesty přes železniční most, když za sebou uslyšeli přijíždět vlak. Protože na mostě nebylo kam uhnout museli seběhnout z mostu. Franta běžel směrem k vlaku a Honza směrem od vlaku. Oběma se podařilo seběhnou z mostu právě v okamžiku, kdy je míjel vlak. Později zjistili, že vlak jel rychlostí 100 km/h. Franta i Honza běželi stejnou rychlostí. Jak rychle běželi?
cesty přes železniční most, když za sebou uslyšeli přijíždět vlak. Protože na mostě nebylo kam uhnout museli seběhnout z mostu. Franta běžel směrem k vlaku a Honza směrem od vlaku. Oběma se podařilo seběhnou z mostu právě v okamžiku, kdy je míjel vlak. Později zjistili, že vlak jel rychlostí 100 km/h. Franta i Honza běželi stejnou rychlostí. Jak rychle běželi?
Řešení ukaž - Aleš a Bedřich si uspořádali závod na kolech. V 7:00 ráno vyrazili. Aleš rychlostí 12 km/h a Bedřich rychlostí 8 km/h. V 9:00 Bedřich dospěl k názoru, že by měl zrychlit. I použil doping (2 piva - časovou ztrátu neuvažujte) a zvýšil svou rychlost na 20 km/h. 4 hodiny poté, co dohonil Aleše, dorazil Bedřich do cíle. V kolik hodin to bylo? Jak dlouhý byl závod?
Řešení ukaž - Koumes s kamarádem Martinem si udělali výlet na kolech. Cestou se zastavili v hospodě, aby se občerstvili. Když se vrátili ke kolům, zjistili, že Martinovo kolo někdo ukradl. Domů to mají ovšem daleko. Pěšky hodinu, na kole 15 minut. Koumes se rozhodl, že se o kolo podělí, a to následujícím způsobem. Jeden půjde pěšky, druhý pojede na kole až na dohled. Tam položí kolo a pokračuje pěšky. Mezitím první dojde ke kolu, nasedne a dohoní druhého, předjede ho opět na dohled, kde položí kolo a role se vyměmí. Takhle se budou střídat až ke Koumesovu domu. Vyšlo jim to úplně perfektně, protože k cíli dorazili současně. Jak dlouho jim trvala cesta?
Řešení ukaž
- Petr chce jet na kole z bodu
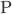 do bodu
do bodu 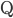 plánovanou rychlostí. Jestliže by zvýšil plánovanou rychlost o 3 m/s, přijel by do bodu
plánovanou rychlostí. Jestliže by zvýšil plánovanou rychlost o 3 m/s, přijel by do bodu 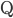 v třikrát kratším čase. Kolikrát méně času mu zabere cesta, pokud zvýší plánovanou rychlost o 6 m/s?
v třikrát kratším čase. Kolikrát méně času mu zabere cesta, pokud zvýší plánovanou rychlost o 6 m/s?
Řešení ukaž - Jestliže student pojede do školy na kole rychlostí 15 km/h, tak přijede o půl hodiny pozdě. Jestliže pojede autobusem rychlostí 40 km/h, tak přijede o dvě hodiny dříve. Jak daleko to má student do školy?
Řešení ukaž - Do města vzdáleného 50 km vyjel cyklista. Vyjel však o 10 minut později, než si naplánoval, a proto jel rychlostí o 0,5 km/h větší, než měl původně v plánu. Do města však přijel v plánovaném čase. Jakou rychlostí měl v plánu jet? Za jak dlouho chtěl původně dojet do města?
Řešení ukaž - Auto ujede vzdálenost mezi 2 městy za 4 hodiny. Kdyby se průměrná rychlost auta zvýšila o 17 km/h, ujelo by auto tuto vzdálenost o 1 hodinu dříve. Urči původní rychlost auta a vzdálenost měst.
Řešení ukaž - Když jede Tomáš do práce na kole konstantní rychlostí 15 km/h, trvá mu cesta o 1 hodinu méně, než když jde pěšky konstantní rychlostí 3 km/h. Jak daleko to má Tomáš do práce?
Řešení ukaž - Martin chodí ze školy obvykle pěšky. Pokud ale jede na kole, jeho průměrná rychlost se zvýší o 10 km/h a doba, kterou mu trvá cesta, se zkrátí o 15 minut. Přijede-li pro něj otec autem, průměrná rychlost se zvýší šestkrát a čas se zkrátí o 20 minut. Jak daleko to má Martin do školy (trasa je ve všech případech stejná)?
Řešení ukaž - Pan Novák jezdí na návštěvu ke svým známým na kole. Vyjíždí vždy ve stejnou dobu a zjistil, že když jede rychlostí 20 km/h, přijede právě v poledne. Když jede rychlostí 30 km/h, přijede v 10:00. Jakou rychlostí musí jet, aby přijel v 11:00?
Řešení ukaž
- Chodec šel na své dvouhodinové procházce nejprve po rovině rychlostí 4 km/h, potom stoupal do kopce rychlostí 3 km/h. Stejnou cestou se vracel zpět. Z kopce šel rychlostí 6 km/h a po rovině opět rychlostí 4 km/h. Kolik kilometrů ušel celkem?
Řešení ukaž - Turista vyrazil na výlet v 9:00 a do cíle došel ve 16:00 téhož dne. Čtvrtinu cesty šel do kopce rychlostí 2 km/h, pak polovinu cesty po rovině rychlostí 4 km/h a poslední část z kopce rychlostí 6 km/h. Kolik kilometrů ušel?
Řešení ukaž - Ke známým do nejbližší vesnice to mám 12 km. Po rovině jedu na kole průměrnou rychlostí 24 km/h, do kopce jedu průměrnou rychlostí 20 km/h a z kopce 30 km/h. Jak dlouho mi bude rvat cesta tam a zpátky?
Řešení ukaž - Cesta z
 do
do  trvá 4:40 hod. a cesta z
trvá 4:40 hod. a cesta z  do
do  trvá 4:00 hod. Auto jede po rovině rychlostí 63 km/h, do kopce rychlostí 56 km/h a z kopce rychlostí 72 km/h. Určete vzdálenost
trvá 4:00 hod. Auto jede po rovině rychlostí 63 km/h, do kopce rychlostí 56 km/h a z kopce rychlostí 72 km/h. Určete vzdálenost 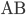 .
.
Řešení ukaž - Vojtík bylo o prázdninách na horách. V 10 hodin ráno vyrazil k vrcholu jedné z nich. Nejprve vedla cesta vodorovně, pak začala rovnoměrně stoupat. Okamžitě po dosažení vrcholu se Vojtík otočil a šel zase toutéž cestou dolů. Domů došel ve 4 hodiny odpoledne. Jakou celkovou vzdálenost Vojtík ušel, když šel do kopce rychlostí 3 km/h, po rovině 4 km/h a z kopce 6 km/h? S přesností na půl hodiny určete, kdy Vojtík dosáhl vrcholu.
Řešení ukaž - Při duatlonu Michal z bodu
 do bodu
do bodu  běžel a zpět jel na kole. Celá cesta mu trvala 1,5 hodiny. Kdyby celou cestu jel na kole, trvala by mu 30 minut. Jak dloho by cesta trvala, kdyby ji celou běžel?
běžel a zpět jel na kole. Celá cesta mu trvala 1,5 hodiny. Kdyby celou cestu jel na kole, trvala by mu 30 minut. Jak dloho by cesta trvala, kdyby ji celou běžel?
Řešení ukaž - Atlet urazí tři kilometry postupně 1 km plaváním, 1 km během a 1 km jízdou na kole. Běží dvakrát rychleji než plave a na kole jede
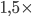 rychleji než běží. Kdyby jel celé tři kilometry na kole, dorazil by do cíle o 10 minut dříve. Za jak dlouho urazí celou trasu?
rychleji než běží. Kdyby jel celé tři kilometry na kole, dorazil by do cíle o 10 minut dříve. Za jak dlouho urazí celou trasu?
Řešení ukaž - Z míst
 a
a  vyjeli současně proti sobě cyklisté. Setkali se 12 km od místa
vyjeli současně proti sobě cyklisté. Setkali se 12 km od místa  a hned pokračovali každý ve své cestě. Když dojeli do míst
a hned pokračovali každý ve své cestě. Když dojeli do míst  ,
,  , otočili se a vraceli se zpět. Podruhé se setkali 6 km od
, otočili se a vraceli se zpět. Podruhé se setkali 6 km od  . Určete rychlost každého cyklisty a vzdálenost
. Určete rychlost každého cyklisty a vzdálenost 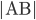 , jestliže víme, že druhý cyklista se navrátil do místa
, jestliže víme, že druhý cyklista se navrátil do místa  o hodinu později než se navrátil prvý cyklista do
o hodinu později než se navrátil prvý cyklista do  .
.
Řešení ukaž - Bob startuje z východního konce a Jane ze západního konce bazénu. Oba plavou dva bazény konstantní rychlostí. Poprvé se potkají 20 m od východního konce a podruhé 18 m od západního konce. Předpokládáme, že při obrátce neztratí žádný čas. Jak dlouhý je bazén?
Řešení ukaž - Dva plavají v bazéně, jehož šířka je 40 m. Jeden plave na šířku, a to středem bazénu. Druhý zase na délku, také středem. Oba plavou stejnou rychlostí a oba začali plavat ve stejnou dobu. Poprvé se potkali po uplavání 510 m. Jaká je délka bazénu?
Řešení ukaž - Tři kamarádi se rozhodli navštívit čtvrtého kamarádu u něj na chatě. První kamarád je sportovně založený a proto vyrazil na kole rychlostí 20 km/h v 8 ráno. Hodinu po něm druhý kamarád vyrazil na motorce rychlostí
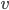 a za další hodinu třetí kamarád autem rychlostí
a za další hodinu třetí kamarád autem rychlostí 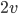 . Všichni tři dorazili k chatě současně. Jak daleko byla chata?
. Všichni tři dorazili k chatě současně. Jak daleko byla chata?
Řešení ukaž
- Loď, jejíž rychlost na klidné vodě je 8 km/h, jela na řece 15 km po proudu a zpět. Celá cesta jí trvala 4 hodiny. Jaká je rychlost vody v řece?
Řešení ukaž - Motorový člun jel proti proudu řeky 16 km a hned se vrátil. Zpáteční cesta mu trvala o 40 minut méně než cesta tam. Jaká je vlastní rychlost člunu, když rychlost proudu je 2 km/h?
Řešení ukaž - Parník jede po proudu 70 km 5 hodin. Pak se vrací a trvá mu to 7 hodin. Kolik kilometrů by ujel tento parník na klidné vodě za 6 hodin?
Řešení ukaž - Přístav
 je 12 km po proudu od přístavu
je 12 km po proudu od přístavu  . Z
. Z  do
do  vyjel výletní parník, jehož rychlost na stojaté vodě by byla 6 km/h. Současně z
vyjel výletní parník, jehož rychlost na stojaté vodě by byla 6 km/h. Současně z  do
do  vyjel motorový člun, jehož rychlost na stojaté vodě by byla 10 km/h. Poté co se lodě setkaly se obě otočily a vrátily se do svých přístavů. Určete rychlost proudu, když se výletní parník vrátil do
vyjel motorový člun, jehož rychlost na stojaté vodě by byla 10 km/h. Poté co se lodě setkaly se obě otočily a vrátily se do svých přístavů. Určete rychlost proudu, když se výletní parník vrátil do  o 1 hodinu později,než motorový člun do
o 1 hodinu později,než motorový člun do  . Čas ztracený při otáčce zanedbejte.
. Čas ztracený při otáčce zanedbejte.
Řešení ukaž - Pepík chodí plavat do řeky. Plave vždy 1 km proti proudu a pak 1 km zpět po proudu. O prázdninách byl u babičky a plaval v jezeře. Plaval vždy stejnou rychlostí a zjistil, že za stejnou dobu, za kterou uplaval 2 km v řece, v jezeře uplave 2,2 km. Kolikrát je Pepík rychlejší než proud řeky?
Řešení ukaž - Dva veslaři ve dvou člunech vyjeli ve 14:55 z přístaviště a veslovali proti proudu řeky. K mostu dojeli spolu, pak se vraceli. Jeden z nich vesloval zpět a vrátil se do přístaviště v 17:55. Druhý se nechal do přístaviště donést proudem a vrátil se v 19:07. Jak dlouho jim trvala plavba z přístaviště k mostu? Rychlost veslování i toku řeky je konstantní.
Řešení ukaž - Voda v řece teče rychlostí 2 m/s. Cesta od přístavu k mostu a zpět trvá malému parníku 33 minut, velkému parníku, který má ve stojaté vodě dvakrát větší rychlost než malý parník, 16 minut. Jak daleko je od přístavu k mostu?
Řešení ukaž - Výletní vzducholoď létá z letiště k pyramidám. Vane-li vítr od letiště k pyramidám rychlostí
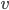 , vykoná vzducholoď cestu tam a zpět za 2 h a 55 minut. Vane-li vítr od pyramid k letišti rychlostí
, vykoná vzducholoď cestu tam a zpět za 2 h a 55 minut. Vane-li vítr od pyramid k letišti rychlostí 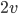 , trvá cesta tam a zpět 3 h a 20 minut. Jak dlouho trvá cesta tam a zpět za bezvětří?
, trvá cesta tam a zpět 3 h a 20 minut. Jak dlouho trvá cesta tam a zpět za bezvětří?
Řešení ukaž - Ivan a Martin jedou na dvoukajaku po řece. Nejprve pádluje Ivan 12 km proti proudu a Martin odpočívá a pak pádluje Martin 12 km zpět po proudu a Ivan odpočívá. Celá cesta jim trvá 4 hodiny. Druhý den si úlohy vymění. Proti proudu pádluje Martin a po proudu Ivan. Celá cesta jim trvá 3 hodiny. Rychlost proudu je 2 km/h. Určete rychlosti, jimiž oba muži pádlují.
Řešení ukaž - Rybář si vyjel na ryby proti proudu řeky motorovým člunem. Když urazil 1 km spadl mu do řeky klobouk. Rybář pokračoval dál v cestě, ale po 5 minutách si vzpomněl, že v klobouku měl rybářský lístek. Otočil člun a vrátil se zpátky pro ztracený klobouk. Dostihl ho přesně v místě odkud na ryby vyrazil. Jak rychle teče řeka? (čas potřebný k otočení člunu zanedbejte).
Řešení ukaž - Vodáci plují s lodí po proudu řeky rychlostí 6 km/h vzhledem k břehu. Rychlost proudu je 2 km/h. V 10:00 míjeli most a jednomu spadl klobouk do vody. Ztrátu objevili ve vzdálenosti 1,5 km od mostu. Otočili se a se stejným úsilím pádlovali proti proudu. V kolik hodin dopluli ke klobouku?
Řešení ukaž - Dvě motorové lodě vyrazily současně z přístaviště na řece. Amazonka dolů po proudu a Vlaštovka proti proudu. Vlastní rychlost (tj. rychlost na stojaté vodě) obou lodí byla stejná. V okamžiku startu spadl z Vlaštovky záchraný kruh a plul po proudu. Za hodinu se obě lodě otočily a jely k sobě. Která z nich byla u záchraného kruhu dříve?
Řešení ukaž - Lodníkovi na motorovém člunu jedoucím proti produ řeky spadl do vody klobouk. Lodník si toho všiml až po 20 minutách, otočil člun a dohonil klobouk dva kilometry od místa, kde mu spadl do vody. Jaká je rychlost proudu?
Řešení ukaž - Petr chodí plavat do řeky. Plave proti proudu 6 minut a pak se vrací na původní místo 3 minuty. Kolik minut by mu trvala celá cesta, kdyby zpět neplaval, ale nechal se unášet proudem?
Řešení ukaž - Tomáš vyjede z metra na jezdících schodech za 40 sekund. Když po jezdících schodech jde, vyjde je za 30 sekund. Za jak dlouho by vyšel po stojících schodech?
Řešení ukaž
- Aleš, Běta a Katka jeli na kolech závod na 10 km. Když Aleš dojel do cíle, byla Běta ještě 2 km od cíle a Katka 4 km od cíle. Jak daleko od cíle byla Katka, když dojela do cíle Běta? Rychlosti všech jsou během závodu konstantní.
Řešení ukaž - Jack and Jane ran the 100 yard dash. When Jane won, Jack was 10 yards behind her. They raced again, but this time Jane started 10 yards behind the starting line. If they both ran at the same rate as in the first race, who won the second race?
Řešení ukaž - Kurýr bězel od konce 80 m dlouhého pochodujícího vojenského útvaru na jeho čelo a pak se stejnou rychlostí vrátil zpět. Během toho se útvar posunul o 150 metrů. Jakou vzálenost uběhl kurýr?
Řešení ukaž - Od námořní lodě, která plula rychlostí 45 km/h vyrazil ve směru plavby průzkumný člun rychlostí 75 km/h. Člun se měl k lodi vrátit za 3 hodiny. Za jakou dobu se musel obrátit a plout zpět k lodi, aby připlul právě včas?
Řešení ukaž - Když jsem ještě chodil do školy, trvala mi cesta z domova do školy 20 minut. Jednou jsem si zapomněl sešit s domácím úkolem. Kdybych šel dále do školy, přišel bych 8 minut před začátkem vyučování. Kdybych se vrátil domů pro sešit, přišel bych 10 minut po zvonění. Jakou část cesty jsem již přešel (předpokládejte, že se pohybuji stále stejnou rychlostí)?
Řešení ukaž - Hasičský vůz vyjel v 10:00 rychlostí 36 km/h k požáru. Současně vyjel i vůz náčelníka rychlostí 60 km/h. Za 18 minut po příjezdu náčelníka přijel i hasičský vůz. Kolik km to bylo k požáru a v kolik hodin dorazil hasičský vůz?
Řešení ukaž - Bonifác a Servác bydlí ve stejném domě. Každé ráno chodí Bonifác i Servác na autobusovou zastávku. Jednou Bonifác zaspal a vyšel z domu o několik minut později. Když byl v desetině cesty na zastávku, všiml si, že Servác je už ve dvou pětinách. Bonifác proto zrychlil. Když mu zbývala jen jedna čtvrtina celé cesty, jeho příteli zbývala jen šestina celé cesty. Kolikrát šel Bonifác rychleji než Servác?
Řešení ukaž - Auto A jede rychlostí 100 km/h a po každých 50 km stojí 10 minut. Auto B, které ze stejného místa vystartovalo současně s autem A, jede bez zastávek stálou rychlostí 50 km/h. Po kterém zastavení bude vzdálenost mezi oběma auty 500 km?
Řešení ukaž - Mezi městy
 a
a  jezdí dva autobusy. Oba mají na trati jedinou zastávku ve městě
jezdí dva autobusy. Oba mají na trati jedinou zastávku ve městě  . Z města
. Z města  do města
do města  je to 60 km, z
je to 60 km, z  do
do  75 km. Oba autobusy vyjedou současně z
75 km. Oba autobusy vyjedou současně z  i
i  proti sobě a na konečnou stanici přijedou opět současně za 90 minut. Přitom ve městě
proti sobě a na konečnou stanici přijedou opět současně za 90 minut. Přitom ve městě  oba stojí přesně 10 minut. Zjistěte, ve kterém místě trati se autobusy setkají.
oba stojí přesně 10 minut. Zjistěte, ve kterém místě trati se autobusy setkají.
Řešení ukaž - Vlak z místa
 do místa
do místa  měl po hodině jízdy poruchu motoru, což mělo za následek snížení rychlosti o 2/5 původní rychlosti. Vlak nakonec přijel do
měl po hodině jízdy poruchu motoru, což mělo za následek snížení rychlosti o 2/5 původní rychlosti. Vlak nakonec přijel do  s dvouhodinovým zpožděním a strojvůdce řekl, že kdyby porucha nastala o 50 km dále, tak by zpoždění bylo o 40 minut menší. Jaká je vzdálenost z
s dvouhodinovým zpožděním a strojvůdce řekl, že kdyby porucha nastala o 50 km dále, tak by zpoždění bylo o 40 minut menší. Jaká je vzdálenost z  do
do  ?
?
Řešení ukaž - Pan Koumes si byl zalyžovat. Na vlek ale byla děsná fronta, a tak se rozhodl vystoupat svah pěšky v blízkosti sedačkového vleku, a pak po stejné trase sjel dolů. Cestou do kopce ho ve stejném směru předjelo 12 sedaček a v protisměru jich potkal 20. Při sjezdu předhonil 3 sedačky a v protisměru potkal 4 sedačky. Rychlost vleku byla stálá 8 km/h, sedačky jsou od sebe stejně vzdálené a jsou neustále v pohybu. Jakou průměrnou rychlostí Kounes stoupal do kopce a jak rychle jej sjížděl?
Řešení ukaž - Dominik pozoroval sedačkovou lanovku. Nejprve zjistil, že spodní stanicí projede každých 8 sekund jedna sedačka. Potom si jednu sedačku vyhlédl, zmáčkl stopky a chtěl změřit jak dlouho potrvá, než se sedačka opět vrátí do spodní stanice. Po 3 minutách a 28 sekundách pustili lanovku rychleji, takže sedačky projížděly stanicí každých 5 sekund. Když pak projížděla Dominikova sedačka, stopky ukazovaly 11 minut a 13 sekund. Kolik sedaček měla lanovka?
Řešení ukaž - Pojízdné schody v metru se pohybují konstantní rychlostí. První osoba vyjde jedoucí schody za 40 sekund a vyjde 40 schodů. Druhá osoba vyjde jedoucí schody za 50 s a vyjde 20 schodů. Kolik schodů je nutné vyjít, pokud eskalátor stojí?
Řešení ukaž - Na dostizích nejvíc diváků tipovalo vítězství koně č.3. Jeho průměrný čas na této dráze byl v minulých dostizích 1 minuta. Kůň se však dnes ve třech čtvrtinách trati splašil, shodil svého žokeje, otočil se a cválal po dráze zpět ke startu. Po 2/3 své zpáteční cesty se znovu otočil a cválal po trati směrem k cílovému sloupku. Jeho žokej mezitím vstal a v okamžiku, kdy se kůň opět rozběhl k cíli, vyběhl mu naproti. Když se oba potkali vyskočil jezdec opět do sedla a společně závod dokončili. Kůň při tomto závodě uběhl celkem 2400 metrů. Bez žokeje cválal kůň jen poloviční rychlostí, oproti té, než když na něm seděl žokej a pobízel ho. Žokej běžel poloviční rychlostí, oproti rychlosti koně bez jezdce. Otázky: (a) Kolik metrů uběhl žokej než opět nasedl na svého koně? (b) Jak dlouho trval tento nepovedený závod?
Řešení ukaž - Petr a Milan jeli tramvají do kina, které je v ulici na trati tramvaje mezi stanicemi
 a
a  . Poměr vzdáleností vchodu do kina od stanic
. Poměr vzdáleností vchodu do kina od stanic  a
a  je 3 : 2. Petr vystoupil na stanici
je 3 : 2. Petr vystoupil na stanici  , Milan na stanici
, Milan na stanici  . Šli stejnou průměrnou rychlostí a ke vchodu do kina přišli oba v témže okamžiku. Vypočítejte, kolikrát byla průměrná rychlost jejich chůze menší než průměrná rychlost tramvaje mezi stanicemi
. Šli stejnou průměrnou rychlostí a ke vchodu do kina přišli oba v témže okamžiku. Vypočítejte, kolikrát byla průměrná rychlost jejich chůze menší než průměrná rychlost tramvaje mezi stanicemi  a
a  .
.
Řešení ukaž