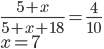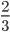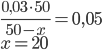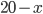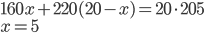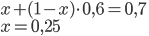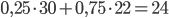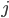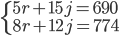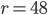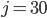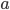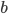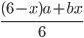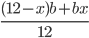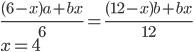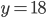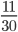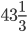- Roztok obsahuje 5 g alkoholu a 18 g vody. Kolik gramů alkoholu musíme do roztoku přidat, aby vznikl 40% roztok alkoholu?
Řešení ukaž - Dva plné sudy kyseliny sírové obsahují 75% a 45% roztoky jsou smíchány. Vznikne 60 litrů 70% roztoku. Jaké byly objemy sudů?
Řešení ukaž - Kolik 5% roztoku kyseliny musí být smícháno s 20% roztokem kyseliny aby vznikly 2 litry 15% roztoku?
Řešení ukaž - Kolik gramů vody se musí vypařit z 50 gramů 3% roztoku soli, aby vznikl 5% roztok soli?
Řešení ukaž - Do 1 litru 20% alkoholu přidáme čistý alkohol tak, že vznikne
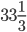 % alkohol. Kolik litrů vody nyní musíme do roztoku přidat, aby vznikl opět 20% alkohol?
% alkohol. Kolik litrů vody nyní musíme do roztoku přidat, aby vznikl opět 20% alkohol?
Řešení ukaž - Nádoba má objem 9 litrů a je plná roztoku 30% alkoholu. Kolik litrů roztoku musíme vylít a nahradit 100% alkoholem, abychom dostali plnou nádobu 65% roztoku?
Řešení ukaž - První nádoba je plná a obsahuje 10% roztok soli. Druhá nádoba má dvakrát větší objem a je plná 5% roztoku soli. Obě nádoby přelijeme do třetí nádoby. Kolika procentní roztok bude ve třetí nádobě?
Řešení ukaž - Vědro má dvakrát větší objem než džbán a je naplněno z deseti procent, džbán je naplněn z třiceti procent. Z kolika procent bude naplněné vědro, přelijeme-li obsah džbánu do vědra?
Řešení ukaž - Kolik 100% alkoholu je nutné přidat do tří litrů 30% alkoholu, abychom dostali 65% alkohol?
Řešení ukaž
- Ze dvou druhů čaje v ceně 160 Kč a 220 Kč za kilogram se musí připravit 20 kg směsi v ceně 205 Kč za l kg. Kolik kilogramů každého druhu je třeba smíchat?
Řešení ukaž - Distributor kávy má dva druhy kávy. První druh stojí 0,40 €/kg, druhý druh stojí 0,65 €/kg. Kolik kilogramů prvního a kolik druhého druhu musí smíchat, aby dostal 200 kg směsi, která má cenu 0,55 €/kg?
Řešení ukaž - Jaká množství kávy I. druhu (za 240,- Kč/kg) a II. druhu za (180,- Kč/kg) je nutné smísit, abychom obdrželi 500 g směsi v ceně 198,- Kč/ kg?
Řešení ukaž - Obchodník prodává sezamová semínka za cenu 200 Kč/kg a slunečnicová semínka v ceně 250 Kč/kg. Prodává taky jejich směs. Kolik kilogramů slunečnicových semínek musí přidat ke dvěma kilogramům sezamových semínek, aby vznikla směs v ceně 237,5 Kč/kg?
Řešení ukaž - Jeden roztok obsahuje 15 \% alkoholu a druhý 30 \% alkoholu. Kolik mililitrů každého roztoku musíme vzít, abychom dostali 600 ml 22\% alkoholu?
Řešení ukaž - Ve dvou lahvích je alkohol: v jedné tříprocentní, ve druhé třicetiprocentní. V jakém poměru musíme oba roztoky smíchat, abychom dostali roztok dvanáctiprocentní?
Řešení ukaž - 500 ml 100% pomerančové šťávy stojí 15 Kč. 1 litr 60% pomerančové šťávy stojí 22 Kč. Smícháním vytvoříme 1 litr 70% pomerančové šťávy. Jaká bude jeho cena?
Řešení ukaž
- Jestliže prodavač v kiosku smíchal 5 litrů rybízového moštu s 15 litry jablečného moštu, získal ovocný nápoj s celkovou cenou 690 Kč. Jestliže tento prodavač smíchal 8 litrů rybízového moštu s 12 litry jablečného moštu, získal ovocný nápoj s celkovou cenou 744 Kč. Vypočítej cenu 1 litru rybízového a 1 litru jablečného moštu.
Řešení ukaž - Ve dvou nádobách je 6 a 12 litrů lihu s různými koncentracemi. Do dvou dalších nádob nabereme z každé nádoby stejné množství lihu, a potom přelijeme do druhé nádoby. Nyní je v obou nádobách stejná koncentrace lihu. Kolik litrů jsme přelili?
Řešení ukaž - 19ti litrová směs obsahuje 1 objemový díl džusu a 18 objemových dílů vody. Když přidáme
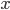 litrů džusu a
litrů džusu a 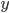 litrů vody, dostaneme 54 litrů směsi obsahující jeden objemový díl džusu a dva objemové díly vody. Určete
litrů vody, dostaneme 54 litrů směsi obsahující jeden objemový díl džusu a dva objemové díly vody. Určete 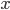 a
a 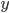 .
.
Řešení ukaž - Při chemickém praktiku studenti míchali dva různé roztoky kyseliny sírové. Když smíchali 3 l silnějšího a 2 l slabšího roztoku, dostali 42% roztok. Smícháním 2 l silnějšího a 4 l slabšího roztoku vyrobili 30% roztok. Určete koncentrace původních roztoků.
Řešení ukaž - Máme plnou sklenici vody. Vypijeme
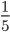 objemu a dolijeme čistým alkoholem. Pak vypijeme
objemu a dolijeme čistým alkoholem. Pak vypijeme 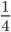 objemu a opět dolijeme čistým alkoholem. Nakonec vypijeme
objemu a opět dolijeme čistým alkoholem. Nakonec vypijeme 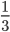 a dolijeme čistým alkoholem. Kolika procentní roztok alkoholu je nyní ve sklenici?
a dolijeme čistým alkoholem. Kolika procentní roztok alkoholu je nyní ve sklenici?
Řešení ukaž - Láhev sirupu stačí na 60 sklenic, když připravujeme nápoje v poměru 1 díl sirupu na 4 díly vody. Kolik sklenic připravíme, když budeme připravovat nápoje v poměru 1 díl sirupu na 5 dílů vody?
Řešení ukaž - Na přípravu oranžového barvy musíme smíchat 3 díly červené barvy se dvěma díly žluté barvy. Na přípravu zelené barvy musíme smíchat 2 díly modré barvy s jedním dílem žluté barvy. Nyní smícháme oranžovou a zelenou barvu v poměru 1:1. Jakou část nové směsi tvoří žlutá barva?
Řešení ukaž - V nádrži je na počátku 8075 litrů vody. Do nádrže přitéká rychlostí 5 litrů/minutu voda a alkohol rychlostí 10 litrů/minutu. Kolik litrů směsi je v nádrži v okamžiku, kdy je v nádrži 10 % alkoholu?
Řešení ukaž - První slitina je složena z mědi a zinku v hmotnostním poměru 5:2, u druhé slitiny je tento poměr 3:4. Kolik kilogramů každé z obou slitin musíme vzít, abychom po jejich společném přetavení získali 28 kg nové slitiny, ve které bude stejně zinku jako mědi?
Řešení ukaž - Po stavení dvou slitin železa a niklu, znichž první měla hmotnost 50 kg a obsahovala 70 % (hmotnostních) niklu, vzniklo 80 kg slitiny s obsahem 60 % niklu. Kolik % niklu bylo v druhé slitině?
Řešení ukaž - Dva odlitky mají dohromady hmotnost 60 kg. První z nich obsahuje 10 kg mědi, druhý 8 kg mědi. Kolik procent mědi obsahuje první odlitek, jestliže u druhého odlitku je počet procent mědi o 15 větší?
Řešení ukaž - Máme skleničku a hrnek, hrnek má třikrát větší objem než sklenička. Ve skleničce je poměr džusu a vody 3:2, v hrnku je poměr 1:2. Vylijeme obsah skleničky i hrnku do džbánu. Jaký je poměr džusu o vody ve džbánu?
Řešení ukaž - Bylo smícháno 3 kg želatinových bonbónů v ceně 160 Kč za 1 kg a 5 kg lékořicových bonbónů v ceně 180 Kč za 1 kg. Kolik Kč stál 1 kg směsi?
Řešení ukaž