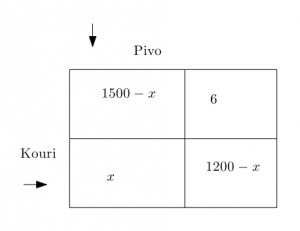
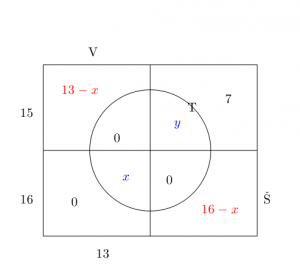
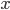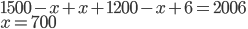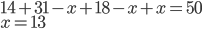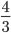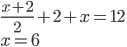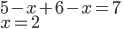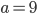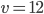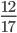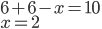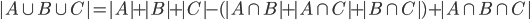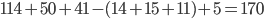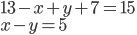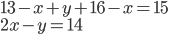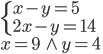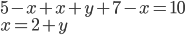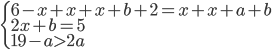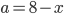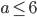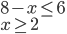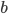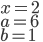- Z průzkumu, ve kterém bylo dotázáno 2006 školáků, vyplývá, že 1500 z nich pije pivo a 1200 kouří cigarety. Kolik z dotázaných dětí pije pivo i kouří, jestliže 6 z nich nepije alkohol ani nekouří?
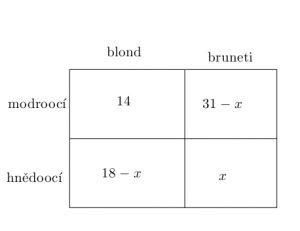
Řešení ukaž - Ve skupině 50 dětí jsou pouze blonďáci a bruneti. Děti jsou modrooké, nebo hnědooké. Čtrnáct modrookých dětí jsou blonďáci. Brunetů je třicet jedna. Hnědookých je osmnáct. Kolik je hnědookých brunetů?
Řešení ukaž - Ve třídě je 34 studentů. Někteří z nich studují historii, někteří zeměpis, někteří oba tyto předměty. Našli se i takoví, kteří si nevybrali ani historii ani zeměpis. Zeměpis studuje 18 studentů. Historii studuje 20 studentů. Oba tyto předměty studuje 8 studentů. Kolik studentů studuje nejvýše jeden z těchto předmětů?
Řešení ukaž - Ve městě jsou 2 výstavy obrazů. V jednom dni navštívilo první z nich 320 osob, druhou z nich 216 osob, z nichž 152 navštívilo jen druhou výstavu. Kolik osob navštívilo jen první výstavu?
Řešení ukaž - Ve třídě je 20 dívek a 15 hochů. Jedna čtvrtina dívek nosí brýle a celkem 20 % žáků ve třídě má brýle. Kolik hochů nenosí brýle?
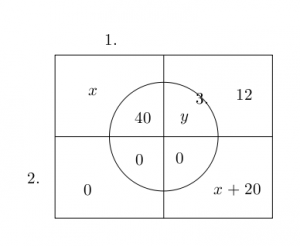
Řešení ukaž - 40 studentů dělalo zkoušky z fyziky a matematiky. 18 studentů neudělalo zkoušku z fyziky. 18 studentů neudělalo zkoušku z matematiky. 8 studentů neudělalo ani jednu zkoušku. Kolik studentů udělalo obě zkoušky?
Řešení ukaž - V místnosti je 30 lidí. 11 z nich mluví francouzsky, 24 mluví anglicky a 3 nemluví ani anglicky ani francouzsky. Kolik lidí mluví anglicky i francouzsky?
Řešení ukaž - Průzkumem mezi 40 studenty se zjistilo, že 27 studentů má rádo dějepis, zeměpis nebo dějepis i zeměpis současně. Z toho 19 studentů má rádo dějepis a 15 studentů má rádo zeměpis. Kolik jich má rádo dějepis i zeměpis zároveň?
Řešení ukaž - Ve škole hraje 50 dívek basketbal a 40 dívek hraje volejbal. Deset dívek dělá oba sporty. Jaký je poměr počtu dívek, které hrají jen basketbal ku počtu dívek, které hrají pouze volejbal?
Řešení ukaž - Při sociologickém výzkumu bylo zjištěno, že v okresním městě Jindřichův Hradec ze 400 respondentů sympatizuje 40 procent s politickým programem strany Modrých a strany Žlutých. Přitom se stranou Modrých sympatizuje o 160 respondentů více než se stranou Žlutých a neexistuje respondent, který by nesympatizoval se stranou Modrých nebo Žlutých. Kolik procent respondentů sympatizuje pouze se stranou Žlutých?
Řešení ukaž - Ve vesnici je 12 sadařů, kteří se specializují na pěstování ovoce. Někteří pěstují jablka zelená a někteří jablka červená. Každý ze sadařů má alespoň jednu z obou variant, šestina z nich má ovšem obě barevné varianty. Těch, kteří mají jen červenou variantu, je dvakrát méně než těch, kteří mají variantu zelenou. Kolik sadařů má zelenou variantu jabloně?
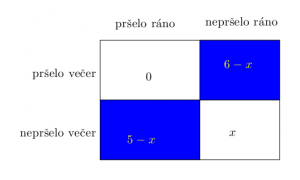
Řešení ukaž - Jana byla na dovolené. Během její dovolené pršelo právě 7 dní. Každý den, kdy pršelo, pršelo buď ráno, nebo večer, ale nikdy ráno i večer. Přesně 5 dní nepršelo večer a přesně 6 dní nepršelo ráno. Kolik dní byla Jana na dovolené?
Řešení ukaž - Od té doby, co si Novákovi koupili štěňátka Punťu a Alíka, chodili každý den na jednu procházku. Někdy s sebou vzali Punťu, někdy Alíka, ale nikdy oba pejsky zároveň. Na osmnácti procházkách s sebou nějakého pejska měli. Punťa zůstal doma čtrnáctkrát, Alík šestnáctkrát. Jak dlouho mají Novákovi Punťu a Alíka?
Řešení ukaž - V obchodě mají 118 dámských klobouků. Klobouky jsou ve dvou barvách, červené, nebo černé a ve dvou verzích, s květinami, nebo bez květin. Celkem mají 44 červených klobouků, 64 klobouků bez květin a 33 černých klobouků s květinami. Kolik mají červených klobouků bez květin?
Řešení ukaž - Z 825 oslovených osob 380 uvedlo, že používá počítač doma nebo v zaměstnání. Počet osob, které používají počítač doma, je dvakrát větší než počet těch, kteří používají počítač doma i v zaměstnání. Počet osob, které používají počítač doma, je také o 40 menší než počet těch, kteří používají počítač pouze v zaměstnání. Kolik oslovených osob používá počítač pouze v zaměstnání?
Řešení ukaž - Z 34 žáků jich dojíždí do školy autobusem o 4 více než těch co jen vlakem. Autobusem a vlakem jich dojíždí o 1 více než těch co nejezdí žádným z obou dopravních prostředků.Vlakem nejezdí 15 žáků.Kolik jezdí jen autobusem a kolik jezdí jen vlakem?
Řešení ukaž - V hotelu se ubytovalo 20 hostů. Česky jich mluvilo o 4 více než anglicky. Jedním nebo žádným z těchto dvou jazyků mluvilo 15 hostů. Alespoň jedním z těchto dvou jazyků mluvilo 17 hostů. Kolik hostů mluvilo česky?
Řešení ukaž - Ze 129 studentů prvního ročníku chodí do menzy pravidelně na oběd nebo večeři 116 studentů, 62 studentů dochází nejvýše na jedno z těchto jídel. Přitom na obědy chodí o 47 studentů víc než na večeři. Kolik ze studentů chodí na obědy?
Řešení ukaž - K cestě je připraveno sto osob. Deset z nich neumí ani francouzsky, ani německy. Sedmdesát pět osob umí německy, osmdesát tři osob umí francouzsky. Kolik turistů ovládá oba dva jazyky?
Řešení ukaž - Ve třídě je 40 žáků. 10 % z nich nosí brýle. Polovina třídy nosí čepici. Těch, kteří nenosí ani brýle, ani čepici je 9 krát více, než těch, kteří nosí i brýle i čepici. Kolik žáků nosí i brýle i čepici?
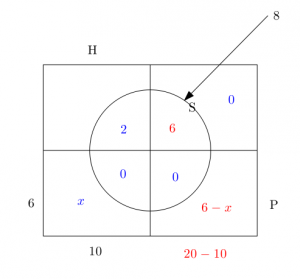
Řešení ukaž - Víme, že 25 % všech moudrých lidí je krásných. Polovina všech krásných lidí je moudrá. A 25 % všech lidí není ani krásných, ani moudrých. Kolik % všech lidí je krásných i moudrých?
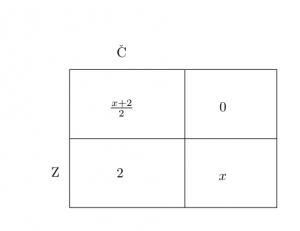
Řešení ukaž - Stejný počet studentů a učitelů se zúčastnil průzkumu, kde odpovídali na jednu otázku (ano-ne). 60 % těch, co odpověděli "ano" byli učitelé a 80 % těch, co odpověděli "ne" byli studenti. Kolik % studentů odpovědělo "ano"?
Řešení ukaž - Třída, ve které jsou chlapci i dívky, psala test. Právě
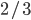chlapců a právě 
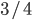dívek test napsaly. Přitom počet chlapců, kteří test napsali, byl stejný jako počet dívek, které test napsaly. Jaká část celé třídy napsala test?
Řešení ukaž - Ve skupině jsou 14tiletí a 15tiletí studenti. 80 % studentů jsou chlapci. 25 % dívek je 14tiletých. 15tiletých studentů je třikrát více než 14tiletých. Kolik procent studentů jsou 14tiltí chlapci?
Řešení ukaž - Průzkumu se zúčatnilo 400 lidí. 223 z nich má kolo, 172 má inline brusle a 87 nemá ani kolo, ani inline brusle. Kolik lidí z průzkumu má kolo i inline brusle?
Řešení ukaž - Organizátor výstavy „Stavím, stavíš, stavíme“ rozdělil expozici do dvou částí. Protože ho zajímala reakce návštěvníků výstavy, vyplnil každý návštěvník při odchodu jednoduchý dotazník. Vyplynuly z něj tyto zajimavé skutečnosti:
- 96 % návštěvníků, kterým se líbila první část, se líbila i druhá část,
- 60 % návštěvníků, kterým se líbila druhá část, se líbila i první část,
- 59 % návštěvníků se nelíbila ani první část, ani druhá část.
Kolik procent všech návštěvníků uvedlo, že se jim líbila první část výstavy?
Řešení ukaž
- Ve škole je 20 učitelů. 10 učí humanitní vědy, 8 učí sociální vědy a 6 učí přírodní vědy. Dva učitelé učí humanitní i sociální vědy, ale žádný neučí sociální a přírodní vědy. Kolik učitelů učí humanitní i přírodní vědy?
Řešení ukaž - 200 studentů dělalo zkoušky z češtiny, matematiky a fyziky. 114 studentů udělalo češtinu, 50 studentů udělalo matematiku a 41 studentů udělalo fyziku. Zkoušku z češtiny i matematiky udělalo 14 studentů, z matematiky i fyziky 15 studentů a z češtiny i fyziky 11 studentů. Všechny tři zkoušky udělalo 5 studentů. Kolik studentů neudělalo ani jednu zkoušku?
Řešení ukaž - Ve škole jsou tři kroužky: fotografický, motoristický a šachový. Do fotografického kroužku chodi 16 žáků, do motoristického 17 žáků a do šachového 14 žáků. 8 žáků chodí současně do fotografického i motoristického, 6 do fotografického i šachového, 4 motoristického a šachového. 3 žáci navštěvují všechny tři kroužky a 4 žáci nechodí do žádného kroužku. Kolik je žáků ve třídě?
Řešení ukaž - Ve třídě udělalo 20 studentů zkoušku z matematiky, 18 z fyziky a 10 z češtiny. 2 studenti udělali zkoušky ze všech tří předmětů. 13 studentů udělalo zkoušky z právě dvou předmětů a 9 studentů neudělalo zkoušku z žádného z těchto předmětů. Kolik studentů je ve třídě?
Řešení ukaž - Ve škole je 100 studentů. 50 z nich hraje fotbal, 45 hraje basketbal a 50 hraje volejbal. Pouze 15 studentů dělá všechny tři sporty a každý dělá aspoň jeden sport. Kolik studentů dělá právě dva sporty?
Řešení ukaž - Na fotbalovém utkání byl neznámý počet diváků. 13 diváků mělo vlajku, 16 jich mělo šálu, 7 diváků nemělo nic. Někteří diváci měli trumpetu. Jen jednu věc mělo 15 diváků, právě dvě věci neměl nikdo. Šálu nemělo 15 diváků. Kolik diváků mělo trumpetu? Kolik diváků mělo všechny tři věci? Kolik bylo na utkání celkem diváků?
Řešení ukaž - Na hřišti si hrálo 26 dětí. 11 dětí mělo autíčko, 17 dětí mělo lopatičku. Jen bábovičku mělo 5 dětí. Nikdo neměl autíčko a bábovičku zároveň. Každé dítě mělo aspoň jednu hračku. Právě dvě hračky mělo 15 dětí. Kolik dětí mělo bábovičku? Kolik dětí mělo všechny tři hračky? Kolik dětí mělo jen lopatičku?
Řešení ukaž - Při zkoušce počítali studenti tři příklady. Třetí příklad vyřešilo 21 studentů, první příklad 23 studentů a druhý příklad také 23 studentů. Dva studenti nevyřešili žádný příklad, všechny tři příklady vyřešilo 7 studentů. První a druhý příklad vyřešilo 15 studentů, první a třetí příklad vyřešilo 12 studentů. Druhý nebo třetí příklad vyřešilo 31 studentů. Kolik studentů psalo zkoušku?
Řešení ukaž - Písemná práce z matematiky, které se zúčastnilo 35 studentů, obsahovala tři úlohy. Dva studenti vyřešili jenom první úlohu a tři jenom druhou. První a druhou úlohu vyřešilo 16 studentů, druhou a třetí 14 studentů. Všechny úlohy vyřešilo 10 studentů, první nebo třetí 31 studentů a 3 studenti nevyřešili ani první, ani druhou úlohu. Kolik studentů vyřešilo:
(a) aspoň dvě úlohy
(b) aspoň jednu úlohu?Řešení ukaž -
Delegátka nabídla 45 účastníkům zahraničního pobytového zájezdu tři fakultativní výlety. První výlet si vybralo 23 rekreantů, první i druhý 7 rekreantů. 15 účastníků jelo na první výlet a přitom nejelo na třetí výlet, 10 jelo pouze na první výlet a 3 pouze na třetí výlet. Právě jeden z výletů si zvolilo 17 osob. Jedna třetina z počtu účastníků se nezúčastnila žádného výletu. Kolik účastníků si vybralo
a) jenom druhý výlet
b) druhý výlet
c) právě dva výlety
d) druhý a třetí výlet a přitom si nevybralo první výlet?Řešení ukaž - Ve třídě je 22 chlapců, kteří se všichni věnují nějakému sportu: 19 fotbalu, 5 karate a 10 hokeji. Přitom všichni karatisté jsou fotbalisty a 3 hokejisté jsou zároveň karatisté. Kolik chlapců hraje pouze hokej, jestliže 10 chlapců hraje jen fotbal?
Řešení ukaž - Při dopravní kontrole bylo zkontrolováno 800 řidičů. Mezi nejčastější přestupky patřilo překročení stanovené rychlosti, nesprávná jízda v jízdních pruzích a špatný technický stav vozidla. Žádného z uvedených přestupků se nedopustilo 500 řidičů, všechny tři přestupky byly zjištěny u 2 řidičů a u 43 řidičů byly zjištěny právě dva z těchto přestupků. Rychlost překročilo 187 řidičů a špatný technický stav byl zjištěn ve 110 případech. 75 řidičů mělo vozidlo ve špatném technickém stavu a přitom se nedopustilo žádného dalšího přestupku. Přestože 27 řidičů mělo vozidlo ve špatném technickém stavu, překročilo povolenou rychlost.
(a) U kolika řidičů byla zjištěna nesprávná jízda v jízdních pruzích?
(b) Kolik řidičů se dopustilo právě jednoho z uvedených přestupků?Řešení ukaž
- Každý José je Rodrigo. Polovina ze všech Španělů jsou Rodrigové. Polovina ze všech Rodrigů jsou José. Celkem máme 40 Španělů a 30 José. Přitom žádný Španěl není José. Kolik Rodrigů není ani Španěl, ani José?
Řešení ukaž - Všichni Nguyenové jsou Tuanové. Jedna třetina Tuanů jsou Nguyenové. Polovina všech Trangů jsou Tuanové. Jeden Trang je Nguyen. Osm Trangů jsou Tuanové. Tuanů je 90. Kolik Tuanů není ani Nguyen, ani Trang?
Řešení ukaž
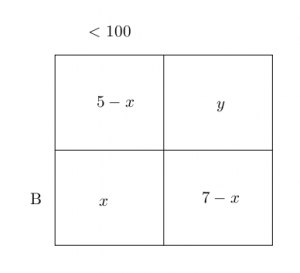
- V obchodě mají různých 10 kravat. Pět z nich stojí méně než 100 Kč. Sedm z nich je bílých. Jaký je nejmenší počet bílých kravat levnějších než 100 Kč?
Řešení ukaž - Test měl 3 úlohy. 80 % studentů vyřešilo 1. úlohu, 75 % 2. úlohu a 70 % 3. úlohu. Jaká nejmenší část studentů musela vyřešit všechny tři úlohy?
Řešení ukaž - Studenti si vybírali přednášky z chemie, fyziky a algebry. Počet studentů byl ve všech předmětech stejný. Počet studentů, kteří si vybrali právě dva předměty byl stejný pro všechny tři páry předmětů, a tento počet byl třikrát větší než počet těch, kteří si vybrali všechny tři předměty. Počet studentů, kteří studovali fyziku (a případně i další předměty) byl pětkrát větší než počet těch, kteří si vybrali chemii a algebru, ale ne fyziku. Jaký nejmenší počet studentů mohl být ve škole?
Řešení ukaž
- Klub turistů zorganizoval tři výlety. Ze 120 členů klubu nikdo neabsolvoval dva výlety za sebou, ale dvou výletů se zúčastnila třetina členů. Aspoň jednoho výletu se zúčastnilo 90 % členů klubu. Na druhém výletu bylo o 20 členů méně než na prvním a o 8 méně než na třetím. Kolik členů absolvovalo jednotlivé výlety?
Řešení ukaž - V testu byly tři příklady. Pět studentů vyřešilo všechny příklady, dva studenti žádný. První příklad vyřešilo 20 studentů, druhý 19 studentů a třetí 17. První a druhý vyřešilo 12 studentů, první a třetí také 12 a druhý a třetí 7 studentů. Kolik studentů se účastnilo testu?
Řešení ukaž - Delegátka nabídla 45 účastníkům zahraničního pobytového zájezdu tři fakultativní výlety. První výlet si vybralo 23 rekreantů, první i druhý 7 rekreantů. 15 rekreantů jelo na první výlet a při tom nejelo na třetí výlet, 10 jelo pouze na první výlet a 3 pouze na třetí výlet. Právě jeden z výletů si zvolilo 17 osob. Jedna třetina z počtu účastníků se nezúčastnila žádného výletu. Kolik účastníků si vybralo:
(a) jenom druhý výlet
(b) druhý výlet
(c) právě dva výlety
(d) druhý a třetí výlet a přitom si nevybralo první výlet?Řešení ukaž - Mezinárodní konference o teorii množin se účastní celkem 134 matematiků, z nich každý ovládá alespoň jeden z těchto jazyků: ruštinu, francouzštinu, angličtinu. 15 z nich ovládá všechny tři jazyky, angličtinu zná o 28 účastníků více než ruštinu. Těch, kteří ovládají ruštinu a francouzštinu, ale neznají angličtinu, je pětkrát méně než těch, kteří znají pouze angličtinu. Účastníků konference, kteří znají jenom ruštinu, je třikrát více než těch, kteří ovládají ruštinu i angličtinu, ale neznají francouzštinu. Těch, kteří znají jenom francouzštinu, je právě tolik, jako těch, kteří ovládají jenom angličtinu. Účastníků, kteří ovládají angličtinu a ruštinu, ale neznají francouzštinu, je o 18 méně než těch, kteří neumí rusky, ale znají francouzsky a anglicky. (a) Kolik lidí ovládá právě dva jazyky? (b) Kterým jazkem mluví nejvíce lidí?
Řešení ukaž - 130 žáků se učí angličtinu, němčinu nebo francuzštinu. Každý žák se učí aspoň dva jazyky, přičemž 20 se učí všechny tři. Angličtinu a němčinu se učí přesně tolik žáků jako angličtinu a francouzštinu. Pouze němčinu a francouzštinu se učí o 10 žáků méně než je těch, kteří se učí všechny tři jazyky. Kolik žáků se učí jednotlivé jazyky?
Řešení ukaž - Každý ze třiceti studentů umí aspoň jeden z těchto tří jazyků: čínsky, katalánsky nebo velšsky. Čínsky umí 25 studentů, z nichž 6 umí i katalánsky. Počet studentů, kteří umí všechny 3 jazyky, je stejný jako počet studentů, kteří umí jenom katalánsky, a také stejný jako počet studentů, kteří umí jenom velšsky. Studentů, kteří umí katalánsky, je o 2 méně než těch, co umí velšsky. Studentů, kteří umí jenom čínsky, je více než dvakrát tolik než těch, co umí jenom čínsky a velšsky. Kolik studentů mluví jednotlivými jazyky?
Řešení ukaž
