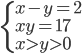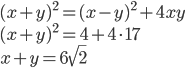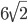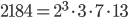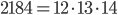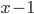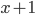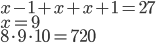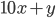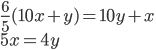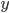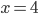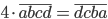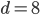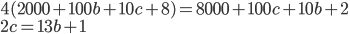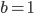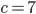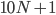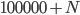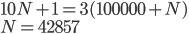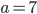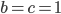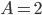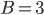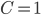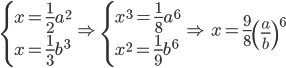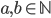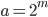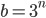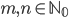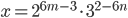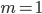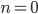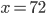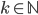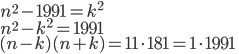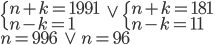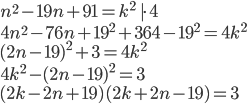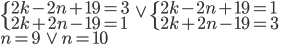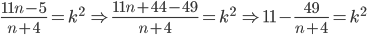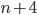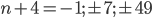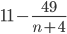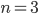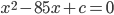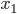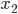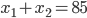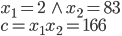- Které přirozené číslo se umocněním na druhou zvětší o 500 %?
Řešení ukaž - Průměr padesáti čísel je 76. Čtyřicet z těchto čísel má průměr 80. Jaký je průměr zbylých deseti čísel?
Řešení ukaž - Rozdíl dvou kladných čísel je 2 a jejich součin je 17. Kolik je jejich součet?
Řešení ukaž - Odečtením rozdílu druhých mocnin dvou sousedních přirozených čísel od rozdílu jejich třetích mocnin dostaneme číslo 30. Která jsou to čísla?
Řešení ukaž - Součin tří po sobě jdoucích čísel je 2184. Jaký je jejich součet?
Řešení ukaž - Součet tří za sebou jdoucích přirozených čísel je 27. Jaký je jejich součin?
Řešení ukaž - Určete součet tří po sobě jdoucích přirozených čísel takových, že součet prvního a třetího je 368.
Řešení ukaž - Když ve dvouciferném čísle změníme pořadí cifer, jeho hodnota se zvětší o 20 %. Jaké je to číslo?
Řešení ukaž - Když ve dvouciferném čísle prohodíme cifry, vznikne číslo, které je o 75 % větší, než původní číslo. Určete největší takové číslo.
Řešení ukaž - Ciferný součet dvouciferného čísla je 15. Jestliže toto číslo zvětšíme o 27, dostaneme číslo zapsané stejnými číslicemi, ale v obráceném pořadí. Určete toto číslo.
Řešení ukaž - Dvojciferné číslo má součet cifer 8. Součin tohoto čísla a čísla, které z něho vznikne obrácením pořadí, je 1855. Určete uvažované číslo.
Řešení ukaž - Když u dvojciferného čísla prohodíme cifry a k nově získanému číslu přičteme 3, dostaneme dvojnásobek původního čísla. Určete původní číslo.
Řešení ukaž - Je dáno číslo menší než 50. Když toto číslo zdvojnásobíme a odečteme 12, dostaneme číslo, které má stejné číslice jako původní číslo, ale v opačném pořadí. Určete původní číslo.
Řešení ukaž - Jestliže přečteme určité dvouciferné číslo zprava doleva, bude nové číslo čtyřiapůlkrát větší než dané číslo. O které číslo se jedná?
Řešení ukaž - Součin tří za sebou jdoucích čísel je osmkrát větší než jejich součet. Určete tato čísla.
Řešení ukaž - Součin tří za sebou jdoucích přirozených čísel je 33 krát větší než jejich součet. Určete tato čísla.
Řešení ukaž - Součin tří za sebou jdoucích přirozených čísel je 40 krát větší než jejich součet. Která jsou to čísla?
Řešení ukaž - Jsou dána čtyři za sebou jdoucí přirozená čísla. Součet třetích mocnin prvních tří čísel se rovná třetí mocnině čtvrtého čísla. Která jsou to čísla?
Řešení ukaž - Součin čtyř různých přirozených čísel, z nichž přesně tři jsou lichá, je
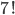 . Součet těchto čtyř čísel je 63. Která jsou to čísla?
. Součet těchto čtyř čísel je 63. Která jsou to čísla?
Řešení ukaž - Máme pět za sebou jdoucích přirozených čísel. Součet prvních čtyř je roven trojnásobku pátého čísla. Která jsou to čísla?
Řešení ukaž - Pět za sebou jdoucích celých čísel má následující vlastnost: součet druhých mocnin prvních tří čísel se rovná součtu druhých mocnin zbývajících dvou čísel. Určete všechny pětice, které mají tuto vlastnost.
Řešení ukaž - Je dáno 6 za sebou jdoucích přirozených čísel. Součet druhého, čtvrtého a pátého čísla je 41. Jaký je součet třetího a šestého čísla?
Řešení ukaž - Jestliže napíšeme číslice ve čtyřciferném čísle v opačném pořadí, dostaneme číslo 4 krát větší. Určete všechna čísla, která mají tuto vlastnost.
Řešení ukaž - Když čtyřciferné číslo
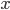 vynásobíme 9, dostaneme jiné čtyřciferné číslo, které má cifry v obráceném pořadí než číslo
vynásobíme 9, dostaneme jiné čtyřciferné číslo, které má cifry v obráceném pořadí než číslo 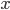 . Určete číslo
. Určete číslo 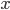 .
.
Řešení ukaž 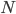 je pěticiferné číslo. Když napíšeme 1 na konec tohoto čísla, dostaneme číslo třikrát větší, než když napíšeme 1 na začátek čísla
je pěticiferné číslo. Když napíšeme 1 na konec tohoto čísla, dostaneme číslo třikrát větší, než když napíšeme 1 na začátek čísla 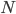 . Určete číslo
. Určete číslo 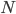 .
.
Řešení ukaž - Číslo
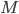 je dvouciferné přirozené číslo. Číslo
je dvouciferné přirozené číslo. Číslo 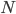 získáme z čísla
získáme z čísla 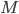 tak, že vyměníme pořadí číslic. Víme, že rozdíl
tak, že vyměníme pořadí číslic. Víme, že rozdíl 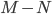 je kladná druhá mocnina přirozeného čísla. Kolik čísel
je kladná druhá mocnina přirozeného čísla. Kolik čísel 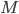 existuje?
existuje?
Řešení ukaž - Rozdíl, součet a součin dvou čísel je v poměru 1:7:18. Která jsou to čísla?
Řešení ukaž - Poměr rozdílu, součtu a součinu dvou čísel je 1:7:24. Která jsou to čísla?
Řešení ukaž - Najděte 4-ciferné číslo, které má všechny následující vlastnosti:
(a) ciferný součet je roven 10,
(b) rozdíl tohoto čísla a čísla napsaného pozpátku je 3087,
(c) součet prvních dvou cifer je o 4 větší než součet posledních dvou,
(d) součet první a čtvrté cifry je stejný jako součet druhé a třetí cifry.Řešení ukaž - Určete tři přirozená čísla
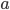 ,
, 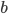 ,
,  , pro která platí
, pro která platí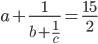
Řešení ukaž - Určete tři přirozená nesoudělná čísla
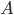 ,
, 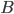 ,
, 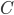 , pro která platí
, pro která platí 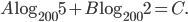
Řešení ukaž - Pro jakou cifru
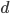 je číslo
je číslo 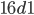 druhá mocnina přitozeného čísla?
druhá mocnina přitozeného čísla?
Řešení ukaž - Najděte nejmenší přirozené číslo, které se rovná jedné polovině druhé mocniny a zároveň jedné třetine třetí mocniny.
Řešení ukaž - Určete všechna
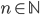 taková, že číslo
taková, že číslo 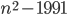 je druhá mocnina přirozeného čísla.
je druhá mocnina přirozeného čísla.
Řešení ukaž - Určete všechna
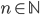 taková, že číslo
taková, že číslo 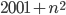 je druhá mocnina přirozeného čísla.
je druhá mocnina přirozeného čísla.
Řešení ukaž - Určete všechna
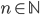 taková, že číslo
taková, že číslo 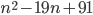 je druhá mocnina přirozeného čísla.
je druhá mocnina přirozeného čísla.
Řešení ukaž - Určete všechna
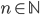 taková, že číslo
taková, že číslo 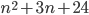 je druhá mocnina přirozeného čísla.
je druhá mocnina přirozeného čísla.
Řešení ukaž - Najděte všechna kladná celá čísla
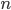 , pro která je číslo
, pro která je číslo 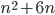 druhou mocninou přirozeného čísla.
druhou mocninou přirozeného čísla.
Řešení ukaž - Najděte nejmenší přirozené číslo
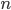 takové, že čísla
takové, že čísla 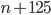 a
a 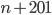 jsou současně druhou mocninou přirozeného čísla.
jsou současně druhou mocninou přirozeného čísla.
Řešení ukaž - Určete všechna
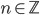 taková, že číslo
taková, že číslo
je přirozené číslo.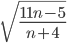
Řešení ukaž - Nechť
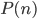 a
a 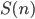 označují postupně ciferný součin a součet čísla
označují postupně ciferný součin a součet čísla 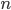 . Například
. Například 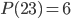 a
a 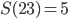 . Pro dvouciferné číslo
. Pro dvouciferné číslo 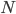 platí
platí
Určete číslici na místě jednotek čísla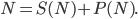
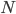 .
.
Řešení ukaž - Petr si myslí dvojmístné číslo. Když tohle číslo napíše dvakrát za sebou, vznikne čtyřmístné číslo, které je dělitelné devíti. Když totéž číslo napíše třikrát. za sebou, vznikne šestimístné číslo, které je dělitelné osmi. Zjistěte, jaké číslo si může Petr myslet.
Řešení ukaž - Dvouciferné číslo vydělíme číslem, které vznikne z původního čísla přehozením cifer. Výsledek je 3 a zbytek 5. Jaké bylo původní číslo?
Řešení ukaž - Je dáno šesticiferné číslo, které končí číslicí 4. Když tuto číslici přesuneme na začátek daného čísla (před jeho první cifru), vznikne nové číslo, které je čtyřnásobkem původního. Jaké je to číslo?
Řešení ukaž - Když k danému přirozenému číslu přičteme součet jeho cifer, dostaneme 101. Která čísla mají tuto vlastnost?
Řešení ukaž